Trygonometria Pati: 1.Wiedząc, że α jest kątem ostrym i sinα = ^√5₅ Oblicz tgα 2. Wiedząc, że tgα = ¹₃, oblicz wartość wyrażenia 5 (2sin²α−1) 3. Czy istnieje kąt ostry α taki, że: sinα=^√3₃ i tgα ²₃ Bardzo proszę o pomoc w tych zadaniach. Z góry dziękuje i pozdrawiam

Pati: Błagam nich ktoś odpisze...

Rafał274: 1)

	2√5
cosα = √1 − sin2α = √1 − (√5/5)2 =
	5

	sinα		1
tgα =		=
	cosα		2

Rafał274: 3)

	√6
cos a =
	3

	√2
Wtedy tan a =
	2

Zatem nie istnieje taki kąt

Rafał274: 2 nie wiem, ale według komputera wyjdzie −4.

Mila:

	sinα
1) tgα=
	cosα

	√5
(		)2+cos2α=1
	5

	4
cos2α=
	5

	2
cosα=
	√5

	√5		2
tgα=		:		dokończ
	5		√5

	sinα		1
2) tgα=		=
	cosα		3

cosα=3sinα podstaw do jedynki trygonometrycznej i oblicz sinα

	sinα		2
3)tgα=		=
	cosα		3

3sinα=2cosα 2cosα=√3

	√3
cosα=		podstaw do jedynki tryg. ma wyjść 1.
	2

Beti:

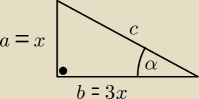
	1		a
tgα =		=		to: a=x, b= 3x
	3		b

z tw. Pit. c² = (3x)² + x² c² = 10x² c = √10x

	a		x		1		√10
sinα =		=		=		=
	c		√10x		√10		10

	1		1		1		9
5(2sin2x − 1) = 5(2*		− 1) = 5(		− 1) =		− 5 = −4		= −4.9
	100		50		10		10

Pati: Dziękuję wam kochani bardzo * Już próbuję to ogarnąć

Ajtek: Beti zgubiłaś 10 w liczniku

	√10
sinx=
	10

	√10
...=5(2*(		)2−1)=...
	10

Pati: Beti dlaczego w pierwszym zadaniu cos²α = ⁴₅ a następnie cosα=²_√5 Przepraszam ale ciężko u mnie z matą i nie ogarniam podstawowych rzeczy

Ajtek:

	4
cos2x=		/√ pierwiastkujemy stronami
	5

	√4		2
cosx=		⇒ cosx=		, ponieważ √4=2
	√5		√5

Pati: Sorkaa to do Mila miało być

Pati: Ok dzięki Ajtek

Pati: ostatnie pytanie... dlaczego tam jest ⁴₅ skoro jest tam pierwiastek z 5 ?

asdf:

	√5
sinx =
	5

	5		1
sin2x =		=
	25		5

sin²x + cos²x = 1

	1
cos2x = 1 −
	5

	4
cos2x =
	5

	2
cosx =
	√5

	2√5
cosx =
	5