bryły obrotowe milcia002: Błagam o szybką pomoc 1) Oblicz P_c i V stożka którego powierzchnia boczna po rozwinięciu jest wycinkiem koła o promieniu 9 i kącię środkowym 240⁰ 2) Na pomalowanie kuli zużyto 10 litrów farby, Ile potrzeba tej farby aby pomalowac półkule o tym samym r? 3) Przekrój osiowy walca jest prostokątem 3x5. Jaka jest V i P_c?

Beti:

	3
3) 2r = 3 −−> r =		,
	2

h = 5 V = πr²h = ... P_c = 2πr² + 2πrh = ...

milcia002: Dobra to 3 już łapie. i Tu chyba będą 2 przypadki tak? Pierwszy ze wysokość ma 3 a w drugim ze ma 5. Dobrze mówię?

Ajtek: Też bym tak to zrobił, tzn. dwa przypadki.

Beti:

	5
tak, z tym że h = 3, a r =		(bo 5 to średnica)
	2

milcia002: tak tak, dzięki. A umiesz to pierwsze i drugie? Bo tu już zupełnie nie wiem jak to zrobić

Ajtek: 2. kula o promieniu r − 10 litrów półkula o promieniu r −

milcia002: promień 5 i pod wzór, to wszystko?

Ajtek: Nie! Jeżeli na pomalowanie ściany potrzeba x litrów farby, to ile farby potrzeba na pomalowanie połowy tej ściany?

milcia002: a te 10 litrów to nie będzie V?

milcia002: ¹₂ x

Ajtek:

	1
Dokładnie		x.
	2

Nie wlewasz farby do kuli tylko ją malujesz .

milcia002: dobra A dalej jak? Wybacz, ale jak widać nie błyszczę z matematyki więc muszę się dopytać żeby zrozumieć.

Ajtek: Odpowiedz sobie sama: ile l. farby potrzebujesz na pomalowanie półkuli, jeżeli na pomalowanie całej kuli porzebujesz 10 litrów >

milcia002: no 5 litrów. Ale da się to zrobić jakoś matematycznie?

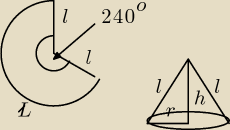
Beti: 1) l = 9

	240		2
Pw =		πl2 =		π*81 = 54π
	360		3

P_w = P_b Ł − długość łuku

	2		4
Ł =		*2πl =		*π*9 = 12π
	3		3

L − obwód podstawy stożka L = 2πr i L = Ł 2πr = 12π r = 6 P_b = πrl = 54π 6πl = 54π l=9 h − możesz obliczyć z tw. Pitagorasa, a potem już V i P_c stożka ze wzorów

milcia002: Dziękuję Beti

Beti: nie 5 litrów , bo w półkuli oprócz połowy sfery dochodzi jeszcze koło

milcia002: no właśnie, to chyba jakoś matematycznie trzeba zrobić.Tak sądzę xd Na tyle to rozgryzłam

Ajtek: Do tego masz napisać obliczenia? Po co? Jeżeli tak to w ten sposób: 1 = kula, 0,5=półkuli 1 − 10 0,5* − x mnożymy "na krzyż" 1*x=0,5*10 x=5

milcia002: Musze napisać na pewno, bo to jest zadanie ze sprawdzianu z brył obrotowych. A nie chce mi się wierzyć że wystarczy coś takiego

Ajtek: Beti ma rację zasugerowałem się sferą .

Beti: Ajtek zaczekaj. Malujesz powierzchnię kuli − czyli sferę. Jeśli przetniesz tę kulę, to do pomalowania będziesz miał połowę sfery i koło będące przekrojem osiowym kuli − a więc więcej niż połowę sfery

Ajtek: W sumie tak, potraktowałem to jak piłkę, którą przecinam w połowie i maluję tylko jej zewnętrzną stronę . O to mi chodziło .

milcia002: A da się to jakoś wytłumaczyć, tak jak "dla debila" xd

milcia002: Beti a nie chcesz może zrobić jeszcze tych zadań, jeśli umiesz jasno wytłumaczyć Bo jak na razie Cie rozumiem.

milcia002: https://matematykaszkolna.pl/forum/140824.html