Funkcja kwadratowa: gucio: Zbiorem rozwiązań nierówności √3−x>x−1 jest zbiór:

gucio: Wiem, że zadanie z pozoru proste, a jednak wychodzi mi ciągle wynik x∊(−1;2), który chyba nie jest poprawny...

MQ: Dobrze ci wyszło! 3−x>0 ⇒ x<3 3−x>(x−1)²=x²−2x+1 x²−x−2>0 (x−2)(x+1)>0 x∊(−1;2)

Maslanek: x<=3 x>=1 3−x>x²−2x+1 x²−x−2>0 (x−2)(x+1)>0 Czyli x∊(2,3> Czy tak?

Maslanek: Dobra bez x>=1... Za dużo kombinowania. Więc x∊(−∞,−1) u (2,3>

MQ: Sorry gucio, Maślanek ma rację!

Ajtek: No to ja swoje "trzy grosze" dorzucę. Wynik MQ jest poprawny, jeżeli chodzi treść zadania, w trakcie rozwiązania coś zostało zjedzone. Maslanek też to zjadł i wynik jest dokładnie przeciwny do treści zadania.

Maslanek: Dobra... Obydwoje jesteśmy głupi x²−x−2<0 Czyli x∊(−1,2)

MQ: Aaa! już widzę! Dobrze myślałem, tylko źle napisałem nierówność! Dzięki Ajtek! Czyli teraz już na pewno (−1;2)

Ajtek: Uff, to się chłopaki poprawili .

gucio: Dziękuje wszystkim! Też mi się wydawało, że to rozwiązanie jest poprawne, jednak w zbiorze zadań było określone jako błędne, dlatego szukałem innych możliwości.. Gdzieś słyszałem, że błędem jest podnoszenie stron do kwadratu w nierówności, ale to raczej niemożliwe..

Ajtek: A jaką masz odpowiedź w zbiorze?

Maslanek: Jest błędne, ale w przypadku kiedy √y<x Wtedy y>=0 i x>=0. Inaczej nie ma to sensu i popełniasz błąd − nierównoważne działania.

Saizou : to może ja to zrobię jeśli nie nie poprzekręcam √3−x>x−1 obustronnie do kwadratu 3−x>(x−1)² 3−x>x²−2x+1 −x²+x+2>0 Δ=1+8=9

	−1−3		−4
x1=		=		=2
	−2		−2

	−1+3		2
x2=		=		=−1
	−2		−2

zatem x∊(−1:2)

Maslanek: wracając do podnoszenia stronami do kwadratu, np. w równościach Weźmy sytuację: −1=1 Gdy podniesiemy: 1=1, co jest prawdziwe Zatem otrzymujemy sprzeczność Przełóżmy to na przypadek ogólny: x=y Jeśli: x<0 i y<0 to możemy podnieść stronami Jeśli: x>=0 i y>=0 to również Jeżeli mamy dwie liczby o przeciwnych znakach to jak najbardziej nie

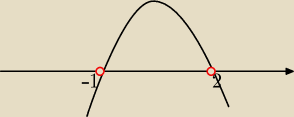
Saizou : i teraz wszystko widać

gucio: I wszystko jasne Dzięki jeszcze raz za pomoc, a zbiór ten zawiera jedynie po trzy odpowiedzi do określonego pytania, z czego każda z nich może być prawdziwa lub fałszywa, dla tego zadania wszystkie były fałszywe, mimo iż zawarta była ta odpowiedź, widać błąd w kluczu

Mila: 1) obie strony nierówności możemy "podnieść" do kwadratu, jęsli są nieujemne, czyli dla x∊<1,3> 2) dla x<1 nierówność jest prawdziwa, bo lewa strona jest dodatnia a prawa ujemna. teraz rozwiążcie i sprawdźcie z odpowiedzią.

Aga1.: √3−x>x−1 gdy 3−x≥0 i x−1<0 x∊(−∞,1) L>0, P<0 nierówność jest prawdziwa dla x<1 gdy 3− x≥0 i x−1≥0,czyli x∊<1.3) możemy podnieść obustronnie do kwadratu 3−x>x²−2x+1 (x−2)(x+1)<0 x∊(−1,2) Uwzględniając dziedzinę x∊(1,2) Odp. x∊(−∞,1)U(1,2) Mam nadzieję, żę nie skopałam

Aga1.: Poprawię przedziały x∊<1,3> (7 linijka od góry) x∊<1.3) od dołu 3 linijka x∊(−∞,2)Od dołu 2 linijka

Mila: Gucio, jaka odpowiedź?

gucio: W zbiorze nie ma niestety odpowiedzi "I wszystko jasne Dzięki jeszcze raz za pomoc, a zbiór ten zawiera jedynie po trzy odpowiedzi do określonego pytania, z czego każda z nich może być prawdziwa lub fałszywa, dla tego zadania wszystkie były fałszywe, mimo iż zawarta była ta odpowiedź, widać błąd w kluczu"

Aga1.: Jeszcze dopatrzyłam się błędu x∊<1,2) trzecia linijka od dołu( o godz.22:19

Mila: Co jest w kluczu?

Mila: Aga1, dobrze.