m.zerowe i dziedzina Piotrek: m.zerowe i dziedzina. Dziedzina R / {4,−5} m.zerowe 3 i −1 dobrze mysle?

	(√x−3)(x+1)
f(x)=
	(x−4)(√x+5)

Piotrek: sprawdzi ktoś, lub wyprowadzi z błędu?

Piotrek: podbijam do góry

Ajtek: D: x≠4 i x−3≥0 i x+5>0 część wspólna tych 3 warunków. M. zerowe zależą od dziedziny.

Saizou : dziedzina jest źle wyznaczona, przyjrzyj się pierwiastkom np √x−3

Piotrek: mógłbyś rozpisać, żebym zrozumiał jak do tego dojść?

Piotrek: czemu x−3 >lub równe 0?

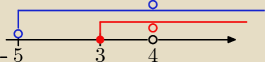
Ajtek: x≠4 x≥3 x>−5 D:x∊≤3;∞)\{4}

Saizou : to co jest pod pierwiastkiem musi być większe bądź równe 0, jeśli pierwiastek jest w mianowniku musi być większe do 0 tak więc x−3≥0 x≥3 x+5>0 x>−5 x−4≠0 x≠4 zatem x∊<3:+∞)

	(√x−3)(x+1)
0=
	(x−4)(√x+5)

0=(√x−3)(x+1) x=−1 albo x=3 i teraz sprawdź czy się mieszczą w dziedzinie

Ajtek: Liczba pod pierwiastkiem parzystego stopnia nie może być mniejsza od zera.

Ajtek: Jeżeli pierwiastek jest w mianowniku to musi być >0.

Saizou : Ajtek jak z przedziału <3:∞) można odjąć 4 skoro 4 już nie ma w tym przedziale?

Ajtek: Saizou nie wywaliłeś 4 z dziedziny .

Ajtek: Czy 4>3

Piotrek: Dziekuje

Ajtek: źle napisałem 3>4

Saizou : jakim cudem ja tam widziałem 8 to ja nie wiem, oj kiepsko już ze mną

Ajtek: Może ktoś w międzyczasie "wyżarł" z 8 kawałek i zrobiło się 3

piotrek: czyli m.zerowe to tylko 3 tak?

Ajtek: Tak .

piotrek: Dzieki jeszcze raz