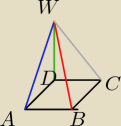
ostroslup zadanko. jok: Podstawą ostrosłupa ABCDW jest kwadrat ABCD o polu 2. Krawędź boczna DW jest wysokością tego ostrosłupa. Długość krawędzi bocznych AW i BW spełniają warunek 2 |BW| = √6 |AW|. Oblicz objętość ostrosłupa. ab=bc = √2

	|AW|
2 |BW| = √6 |AW| , czy		= x?
	|BW|

	√6
BW =		AW
	2

od czego tutaj zacząć?

jok:

jok: Długość boku rombu jest równa , a długości jego przekątnych są równe d₁ i d₂ . Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że a= √d₁d₂

Paula: dorysuj przekatną BD podstawy , otrzymasz 2 trójkaty prostokątne WDB i WAB przekątna podstawy ma 2 cm, bok kwadratu √2 stąd i tw Pitagorasa

⎧	H2+22=BW2
⎩	H2+√22	=AW2

skoro BW=^√2₂ AW to mamy układ

⎧	H2+4=64 AW2
⎩	H2+2=AW2

po rozwiązaniu jeśli sie nie pomyliłam H=2 ale sprawdz.

	1
V=		* pole podst * wys
	3

Paula: dorysuj przekatną BD podstawy , otrzymasz 2 trójkaty prostokątne WDB i WAB przekątna podstawy ma 2 cm, bok kwadratu √2 stąd i tw Pitagorasa

⎧	H2+22=BW2
⎩	H2+√22	=AW2

skoro BW=^√2₂ AW to mamy układ

⎧	H2+4=64 AW2
⎩	H2+2=AW2

po rozwiązaniu jeśli sie nie pomyliłam H=2 ale sprawdz.

	1
V=		* pole podst * wys
	3

asdf: nie rozumiem :

	√2
"skoro BW =		AW"
	2

moim zdaniem :

	6
4 |BW|2 = 6 AW2 >>> BW2 =		AW2
	4

H² + 2 = AW²

	6		4		16
H2 + 4 =		AW2 >>		H2 +		= AW2
	4		6		6

	4		16
H2 + 2 =		H2 +
	6		6

H = 2√2 Niech osoba 3 sprawdzi nasze wyliczenia, dziękuje za podpowiedź.

jok: H² = √2, sprawdzi ktos?

Aga1.:

	√6
BW=		AW
	2

H²=2 H=√2−tak mi wyszło