pole rownolegloboku - 2 boki i przekatna Adam: W równoległoboku ABCD dane są długości odcinków: |AB| = 37 cm, |BC| = 13 cm oraz |AC| = 40 cm. Ile wynosi pole równoległoboku ABCD?

Aga1.: Z twierdzenia cosinusów oblicz cos kąta ostrego równoległoboku, z jedynki trygonometrycznej oblicz sinα i zastosuj wzór P=a*b*sinα Lub oblicz pole trójkąta np. ze wzoru Herona i pomnóż przez 2.

Aga1.: Zdaje się , że kąt ABC jest rozwarty, ale to nic nie zmienia we wzorze

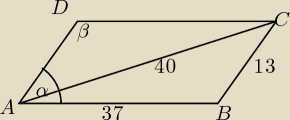
Adam: Jeśli obliczam cos β wychodzą jakieś cuda typu −³¹₄₈₁

Mila:

	13+37+40
p=		=45
	2

P_Δ=√45*(45−13)*(45−37)*(45−40=

Aga1.:

	37+13+40
p=		=45
	2

P_{równoległoboku}=2*P_tr=2√45(45−40)(45−37)(45−13)=2*240=480.

Adam: P_Δ = 240 P_▱ = 480 Dzięki wielkie, wszystko się zgadza.