15 kwi 22:50
think:
| a6 + b2 | | 1 | |
| = |
| absinγ ⇒ sinγ = ... |
| 4 | | 2 | |
c
2 = a
2 + b
2 − 2abcosγ
a później:
15 kwi 22:56
karla: sorry pomyliłam sie S=1/4(a2+b2)
15 kwi 22:59
think: nie ma większego znaczenia, bo i tak podałam Ci jak to policzyć a nie liczyłam tego

15 kwi 23:00
karla: no tak ale to nie wychodzi
15 kwi 23:01
karla: 0= a2 + b2 − 2abcosγ ⇒ c=0
15 kwi 23:01
15 kwi 23:02
think: a jak Ci wyszło 0

?
15 kwi 23:04
karla: 1/4(a2+b2)=1/2(ab)sinγ ⇒ a2+b2=2absinγ ⇒ a2+b2 − 2absinγ=0
15 kwi 23:07
karla: ja chyba źle mysle
15 kwi 23:09
think: a zgadza się, masz rację. Sprawdziłam wzory i nie znajduję błędu póki co.
15 kwi 23:09
think: na pewno taka jest treść tego zadania?
| | (a + b)2 | |
Bo wiesz S = |
| też zmieniłoby sprawę, tylko jeszcze nie wiem jak  |
| | 4 | |
15 kwi 23:14
karla: na pewno
15 kwi 23:15
karla: :(
15 kwi 23:16
think: skąd masz to zadanie?
15 kwi 23:17
karla: z konkursu powiatowego
15 kwi 23:18
think: jest ono dostępne gdzieś na necie?
15 kwi 23:19
karla: obawiam się że nie
15 kwi 23:20
think: dokładnie co to za konkurs jaki powiat, który rok
15 kwi 23:21
think: masz to zadanie na kserówce, czy ręcznie napisane?
15 kwi 23:22
karla: na kserówce
15 kwi 23:22
karla: pojechane są te zadania
15 kwi 23:23
karla: To jest po prostu z poprzednich lat
15 kwi 23:24
Godzio:
Ale pomyliłaś tw. cosinusów:
a
2 + b
2 − 2ab
cosγ = c
2
a
2 + b
2 − 2ab
sinγ = 0

15 kwi 23:25
think: eee tam pojechane, po prostu bardziej wymagające

dlaczego je robisz? Z doświadczenia wiem, że
przeciętni uczniowie nawet nie wiedzą o zadaniach z konkursu powiatowego, bo nie wierzą że z
matmy mogą być konkursy

15 kwi 23:25
think: aaaa Godzio

no widzisz co ja bym bez Ciebie zrobiła!
15 kwi 23:26
think: ale Godzio to i tak nie zmienia faktu, że policzenie cosγ jest jakby skomplikowane, chyba, że
znowu w obliczeniach gdzieś się pomyliłam

15 kwi 23:28
Godzio:
Wyciągam karteczkę, nie ma co

15 kwi 23:30
karla: Dzięki właśnie zrujnowałaś moja wiarę w matematykę.

15 kwi 23:30
think: karla? że jak, wiem, że mam inne poczucie humoru, ale żeby aż tak?

daj spokój, lepiej się
śmiać niż płakać

zresztą jest za późno aby cokolwiek brać na poważnie, poza moimi zachwytami
nad Godziem

15 kwi 23:31
karla: Dobra dobra nie tłumacz sie.

15 kwi 23:33
think: co tam Godzio, też nie chce Ci się wierzyć, ale cos2γ uparcie wychodzi ujemny?
15 kwi 23:37
Godzio:
Posiedzę nad tym dłużej, mam nadzieję, że do 1 się wyrobie

15 kwi 23:38
Godzio:
Ja na razie ustaliłem, że γ ∊ (0o,45o)
15 kwi 23:39
think: hmm no to zostawiam Ci Karlę, bo na mnie pora i pomijam, że mi uparcie wychodzi coś ujemnego
gdzie absolutnie takie być nie może.
15 kwi 23:42
kylo1303: | | a2+b2 | |
Godzio Zaczalem zadanko i tez do tego wniosku doszedlem, co wiecej: sinγ= |
| |
| | 2ab | |

tylko co z tego xD
15 kwi 23:46
Godzio:
No więc tak:
Wyznaczenie reszty kątów pozostawiam wam

15 kwi 23:50
kylo1303: Dzieki Godziu, dobrze ze odwaliles najtrudniejsza robote. Teraz to juz pojdzie z gorki
15 kwi 23:51
karla: Dziekuje

15 kwi 23:52
kylo1303: Na jakim etapie edukacji jest ten konkurs? Liceum czy studia? Bo moze moja lekka kpina
byla nie na miejscu.
15 kwi 23:56
karla: liceum
16 kwi 00:00
Mila: | | a2 | | b2 | | 1 | | a | | b | |
sinγ= |
| + |
| = |
| *( |
| + |
| )=1 |
| | 2ab | | 2ab | | 2 | | b | | a | |
16 kwi 00:02
kylo1303: Kurde, dobre Mila. Nie pomyslalbym o tym xD
16 kwi 00:05
karla: czyli jednak do 1
16 kwi 00:06
Mila: Męczcie się dalej. Jutro zajrzę. Dobranoc.
16 kwi 00:06
Godzio:
Rzeczywiście, ciekawe
16 kwi 00:08
kylo1303: Tzn. nad czym mamy sie meczyc? γ=90o i a=b czyli mamy trojkat prostokatny rownoramienny,
16 kwi 00:09
Godzio:
a
2 + b
2 = 2ab ⇒ a = b
Czyli α = β = 45
o γ = 90
o
16 kwi 00:09
Mila: Godzio, ładne "wykończenie".
16 kwi 13:21







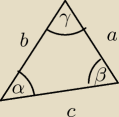
 Pole s trójkąta o bokach długości a i b wyraża się wzorem S=1/4(a6+b2) Znaleźć katy tego
trójkąta
Pole s trójkąta o bokach długości a i b wyraża się wzorem S=1/4(a6+b2) Znaleźć katy tego
trójkąta








 ?
?


 dlaczego je robisz? Z doświadczenia wiem, że
przeciętni uczniowie nawet nie wiedzą o zadaniach z konkursu powiatowego, bo nie wierzą że z
matmy mogą być konkursy
dlaczego je robisz? Z doświadczenia wiem, że
przeciętni uczniowie nawet nie wiedzą o zadaniach z konkursu powiatowego, bo nie wierzą że z
matmy mogą być konkursy
 no widzisz co ja bym bez Ciebie zrobiła!
no widzisz co ja bym bez Ciebie zrobiła!



 daj spokój, lepiej się
śmiać niż płakać
daj spokój, lepiej się
śmiać niż płakać zresztą jest za późno aby cokolwiek brać na poważnie, poza moimi zachwytami
nad Godziem
zresztą jest za późno aby cokolwiek brać na poważnie, poza moimi zachwytami
nad Godziem


 tylko co z tego xD
tylko co z tego xD

