Matura rozszerzona 2011 - czerwiec rumpek: Arkusz maturalny z czerwca 2011 − CKE ROZSZERZENIE Właśnie znalazłem zadania z czerwca, przygotowane dla tych którzy nie mogli pisać w pierwszym terminie: byli chorzy lub co innego. Zadanie 1 (4pkt) Rozwiąż nierówność |2x − 4| + |x − 5| ≥ 12 Zadanie 2 (5pkt) Wyznacz wszystkie wartości parametru m, dla których równanie 2x² − (m − 2)x − 3m = 0 ma dwa różne pierwiastki rzeczywiste x₁, x₂ spełniające warunek: x₁² + x₂² − 2x₁x₂ ≤ 25 Zadanie 3 (5pkt) Ciąg (a,b,c) jest geometryczny. Ciąg (3a + 3, 2b, c − 12) jest arytmetyczny i suma jego dwóch pierwszych wyrazów jest równa trzeciemu. Oblicz a,b,c. Zadanie 4 (4pkt) Rozwiąż równanie 6sin²x + 7cosx − 1 = 0, x∊<0, 2π> Zadanie 5 (4pkt) Dany jest trójkąt ostrokątny ABC o bokach długości a, b, c, i kątach α, β, γ. Wykaż, że:

b2 + c2 − a2		tgβ
	=
a2 + c2 − b2		tgα

Zadanie 6 (3pkt) Wykaż, że nie istnieje wielomian W(x) stopnia trzeciego o współczynnikach całkowitych , który spełnia warunki W(2) = 3 i W(−2) = 2 Zadanie 7 (4pkt) Dany jest trójkąt ostrokątny ABC, w którym |AC| = 5 i |AB| = 8. Pole tego trójkąta jest równe 10√3. Oblicz promień okręgu opisanego na tym trójkącie. Zadanie 8 (5pkt) Punkty A = (−5,5) i C = (8,6) są przeciwległymi wierzchołkami trapezu równoramiennego ABCD w którym AB || CD. Prosta o równaniu y = 2x jest osią symetrii tego trapezu. Oblicz współrzędne wierzchołków B i D oraz pole tego trapezu. Zadanie 9 (3pkt) Przekątne trapezu ABCD przecinają się w punkcie P. Prosta równoległa do podstaw trapezu , przechodząca przez punkt P, przecina ramiona AD i BC odpowiednio w punktach M i N. Wykaż, że |MP| = |NP|. Zadanie 10 (5pkt) Dany jest kwadrat ABCD o boku równym 2. Na bokach BC i CD wybrano odpowiednio punkty E i F, różne od wierzchołków kwadratu, takie, że |CE| = |DF| = x. Oblicz wartość x, dla której pole trójkąta AEF jest najmniejsze i oblicz to pole. Zadanie 11 (4pkt) Spośród wszystkich liczb czterocyfrowych o cyfrach ze zbioru {1, 2, 3} losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wszystkich cyfr wylosowanej liczby jest równa 7. Zadanie 12 (4pkt) W ostrosłupie trójkątnym ABCS o podstawie ABC i wierzchołku S dane są: |AB| = |AC| = |SB| = |SC| = 9 i |AS| = |BC| = 8. Oblicz objętość tego ostrosłupa. ************************************************************************************ Jak dla mnie niektóre zadania powtarzają się z Matury 2010 roku Odnośnie matury podstawowej z matematyki − to chyba jakieś żarty. Było dokładnie to co w tym roku w marcu. To co wyrabia to CKE jest niesamowite. Zadania nie są trudne, według mnie bardziej "niestandardowe" były właśnie w maju. Teraz dali klasyczne. Obstawiamy − które będzie na maturze ? ************************************************************************************

Ajtek: No trudne nie są, jakbym pomyśłał to może ze 4 zrobię .

rumpek: Najciekawsze wydaje się tylko zadanie 8, reszta klasyka

Ajtek: Czy ja wiem czy takie ciekawe? Klasyk z prostopadłościami prostych, i odcinkami, ewentualnie wektory, jak ktoś miał.

rumpek: Lub okręgami

Ajtek: Też można

Święty: Jak już tak zapoczątkowałeś znajdowanie arkuszy to poszukaj tego z maja 2012 Wiesz, ile osób byłoby wdzięcznych...

Ajtek: Dobre Święty

rumpek: podam w maju

Ajtek: rumpek byle przed 8 maja

Aga1.: Ale byłaby afera, ktoś podałby się do dymisji.

TOmek: masz do tego odpowiedzi bo chetnie sobie zrobie te mature?

rumpek:

rumpek: Robimy

rumpek: Zadanie 11 − − − − (4 cyfrowa) Ω = 3 * 3 * 3 * 3 = 3⁴ = 81 Zdarzenie sprzyjające: A = (2, 2, 2, 1) ∨ (3, 2, 1, 1) 1^o (2, 2, 2, 1) = 1 * 4 = 4 możliwości 2^o Wypiszmy dla ułatwienia wszystkie pary: (1, 1, 2, 3) ; (1, 1, 3, 2) ; (1, 2, 3, 1) ; (1, 3, 2, 1) ; (1, 2, 1, 3); (1, 3, 1, 2); (3, 2, 1, 1) ; (2, 3, 1, 1) ; (3, 1, 1, 2) ; (2, 1, 1, 3) ; (3, 1, 2, 1); (2, 1, 3, 1); A = 4 + 12 = 16

	16
P(A) =
	81

Lub można było bez wypisywania: |A| = 4 * 3 * 1 * 1 + 4 * 1 * 1 * 1 = 16

TOmek: masz do tego odpowiedzi bo chetnie sobie zrobie te mature?

Ajtek: Róbcie, mi się nie chce .

rumpek: 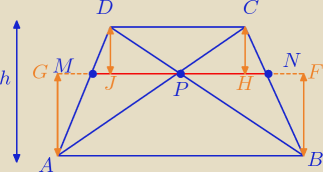Zadanie 9 Oznaczenia takie jak na rysunku. Wpierw udowodnię, że trójkąty △APD i △BPC mają równe pola. Nie jest to trudne, bowiem:

	1
P△ABD =		* |AB| * h
	2

	1
P△ABC =		* |AB| * h, stąd już wynika, że:
	2

P_△ABP + P_△APD = P_△APB + P_△BPC ⇔ P_△APD = P_△BPC Wystarczy teraz porównać pola pozostałych trójkątów:

	1		1
P△APD = P△AMP + P△PMD =		* |MP| * |MA| +		* |MP| * |DJ| =
	2		2

	1		1
=		* |MP| ( |MA| + |DJ| ) =		* |MP| * h
	2		2

	1		1
P△BPC = P△BPN + P△NPC =		* |NP| * |CH| +		* |NP| * |BF| =
	2		2

	1
=		* |NP| * h
	2

Skoro tak jak wykazałem tamte pola są równe, zatem:

1		1
	* |MP| * h =		* |NP| * h
2		2

|MP| = |NP| c.n.u. [można też zrobić z podobieństwa trójkątów]

rumpek: 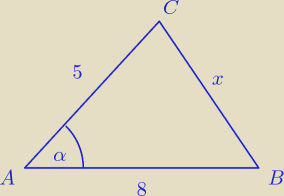Zadanie 7 1^o

	1
P =		* a * b * sinα
	2

10√3 = 5 * 4 * sinα 10√3 = 20sinα

√3
	= sinα
2

α = 60^o (bo kąty ostre same, gdyby nie było informacji trzeba rozpatrywać jeszcze jeden kąt ) 2^o Tw. cosinusów x² = 5² + 8² − 2 * 8 * 5 * cosα

	1
x2 = 25 + 64 − 80 *
	2

x² = 89 − 40 x² = 49, x∊R₊ x = 7 3^o Tw. sinusów

	x
2R =
	sinα

	7
2R =
	√3   2

	14
2R =		/ : 2
	√3

	14√3		7√3
R =		=
	6		3

rumpek: Zadanie 1 |2x − 4| + |x − 5| ≥ 12 1^o x∊(−∞, 2) −(2x − 4) − (x − 5) ≥ 12 −2x + 4 − x + 5 ≥ 12 −3x ≥ 3 x ≤ −1 x∊(−∞; −1> 2^o x∊<2, 5) (2x − 4) − (x − 5) ≥ 12 2x − 4 − x + 5 ≥ 12 x ≥ 11 ∅ 3^o x∊<5, +∞) (2x − 4) + (x − 5) ≥ 12 2x − 4 + x − 5 ≥ 12 3x ≥ 21 / : 3 x ≥ 7 x∊<7, +∞) 4^o Suma rozwiązań: x∊(−∞, −1>U<7, +∞)

Godzio: rumpek z tego co widzę, to 100% z rozszerzenia to pewniak u Ciebie

TOmek: zad. 5 NIestety nie zrobie obraza bo mi sie wiesza, ale łatwo jest sobie narysować c²=b²+a²−2ab*cosβ ⇒ 2ab*cosβ=b²+a²−c² a²=c²+b²−2cb*cosγ ⇒ 2cb*cosγ =c²+b² − a² b²=c²+a²−2ca*cosα ⇒ 2ca*cosα= c²+a²−b²

	tgβ		sinα   cosα		sinα		cosβ
przekształcam sobie		=		=		*
	tgα		sinβ   cosβ		cosα		sinβ

z tw. sinusów

b		c
	=
sinα		sinβ

	sinα*c
sinβ*b=sinα*c ⇒sinβ=
	b

	sinα		cosβ
podstawiam to do tego:		*
	cosα		sinβ

	sinα		cosβ
i to sie równa		*		z tego mamy
	cosα		sinα*c   b

cosβ*b
	rozszerzam ułamek o (2a)
cosα*c

tgβ		cosβ*2ba		b2+a2−c2
	=		=
tgα		cosα*2ca		c2+a2−b2

albo źle przepisałes treść zadania, albo mój dowód jest kijowy

rumpek: Zadanie 2 2x² − (m − 2)x − 3m = 0

⎧	Δ > 0
⎩	x12 + x22 − 2x1x2 ≤ 25

1^o Δ > 0 Δ = (m − 2)² + 24m = m² − 4m + 4 − 24m = m² + 20m + 4 > 0 Δ_m = 20 * 20 − 16 = 400 − 16 = 384 ⇒ √Δ_m = √384 = 8√6

	−20 − 8√6
m1 =		= −10 − 4√6
	2

	−20 + 8√6
m2 =		= 4√6 − 10
	2

m∊(−∞; −10 − 4√6)U(4√6 −10; +∞) 2^o x₁² + x₂² − 2x₁x₂ ≤ 25 x₁² + x₂² = (x₁ + x₂)² − 2x₁x₂ (x₁ + x₂)² − 4x₁x₂ ≤ 25

	m − 2
(		)2 + 2 * 3m ≤ 25
	2

m2 − 4m + 4
	+ 6m ≤ 25 / * 4
4

m² − 4m + 4 + 24m ≤ 100 m² + 20m − 96 ≤ 0 Δ_m = 400 + 384 ⇒ 784 ⇔ √Δ_m = 28

	−20 − 28
m1 =		= −24
	2

	−20 + 28
m2 =		= 4
	2

m∊<−24;4> 3^o Część wspólna: m∊<−24; −10 − 4√6; 4√6 − 10; 4> Straszne pierwiastki

rumpek: 100% nie będzie na bank, robię głupie błędy w obliczeniach

TOmek: dawaj zadanie 5

rumpek: Poprawka: m∊<−24; −10 − 4√6) U (4√6 − 10; 4>

rumpek: Ok, momencik

rumpek: Przecież dobrze masz

rumpek: Aj jednak nie masz dobrze zaraz obadamy

rumpek: 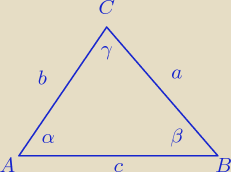Zadanie 5 Tw. cosiunsów: a² = b² + c² − 2bccosα b² = a² + c² − 2accosβ 2bccosα = b² + c² − a²

	b2 + c2 − a2
cosα =
	2bc

2accosβ = a² + c² − b²

	a2 + c2 − b2
cosβ =
	2ac

cosα		b2 + c2 − a2   2bc
	=		=
cosβ		a2 + c2 − b2   2ac

	b2 + c2 − a2		2ac
=		*		=
	2bc		a2 + c2 − b2

	a(b2 + c2 − a2)
=
	b(a2 + c2 − b2)

******************************************************************************************* Tw. sinusów:

	a		a
2R =		⇒ 2Rsinα = a / : 2R ⇔ sinα =
	sinα		2R

	b		b
2R =		⇒ 2Rsinβ = b / : 2R ⇔ sinβ =
	sinβ		2R

tgβ		sinβ     cosβ		sinβcosα
	=		=
tgα		sinα   cosα		sinαcosβ

*******************************************************************************************

	sinβ		b   2R		b		2R		b
1o		=		=		*		=
	sinα		a   2R		2R		a		a

	tgβ		b		cosα
2o		=		*		=
	tgα		a		cosβ

	b		a(b2 + c2 − a2)
=		*		=
	a		b(a2 + c2 − b2)

	b2 + c2 − a2
=
	a2 + c2 − b2

c.n.u.

rumpek: Pomyliłeś się w tw. sinusów

TOmek: ale jakies punkty bym utarał

rumpek: obstawiam, że koło 3

TOmek: rumpek jesli jest podane "o bokach długości a, b, c, i kątach α, β, γ." to chyba ma znaczenie gdzie umiescimy kąty

kylo1303: Zadanie 6 W(x)=ax³+bx²+cx+d, gdzie a,b,c,d∊C W(2)=8a+4b+2c+d=3 W(−2)=−8a+4b−2c+d=2 +−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 8b+2c=5 //:2 4b+c=2,5

	1
c=2 +		− 4b
	2

	1
c= 2−4b +		|| 2−4b=k, k∊C
	2

	1
c=k +		−> z tego wynika ze c nie nalezy do calkowitych
	2

TOmek: zad.3 w(x)=ax³+bx²+cx+d w(2)=8a+4b+2c+d=3 w(−2)=−8a+4b−2c+d=2 −−−−−−−−−−−−−−−−−−−−−−−−−−−− dodaje stronami 4b+2d=6 ⇒ 2b=3−d ⇒ 4b=6−d podstawiam 8a+6−d+2c+d=3 −8a+6−d−2c+d=2 −−−−−−−−−−−−−−−−−−−−− dodaje stronami 12−2d+2d=6 12≠6 moze byc taki dowod

TOmek: zad. 6 powinno być (sprawdzie czy jest ok)

rumpek: Zadanie 3

⎧	b2 = ac
⎨	4b = (3a + 3) + (c − 12)
⎩	(3a + 3) + 2b = c − 12

⎧	b2 = ac
⎨	4b = 3a + c − 9
⎩	3a + 3 + 2b = c − 12

⎧	* b2 = ac
⎨	** b = (3a + c − 9)/4
⎩	***3a + 3 + (3a + c − 9)/2 = c − 12

Zajmijmy się teraz ***:

	3a + c − 9
3a + 3 +		= c − 12 / * 2
	2

6a + 6 + 3a + c − 9 = 2c − 24 9a −3 + c = 2c − 24 9a + 21 = c Rozpatrzmy z kolei **:

	3a + c − 9
b =
	4

	3a + 9a + 21 − 9
b =
	4

	12a + 12
b =
	4

b = 3a + 3 Pozostało podstawić pod *: b² = ac (3a + 3)² = a(9a + 21) 9a² + 18a + 9 = 9a² + 21a 18a + 9 = 21a 9 = 3a a = 3

⎧	a = 3
⎨	b = 12
⎩	c = 48

TOmek: skopałem te zadanie 6...

Eta: 3+2= 6 ?

kylo1303: Tomek − Masz naprawde ciekawe obliczenia, zarowno dodawanie jak i mnozenie

TOmek: W(x)=ax³+bx²+cx+d W(2)=8a+4b+2c+d=3 w(−2)=−8a+4b−2c+d=2 −−−−−−−−−−−−−−−−−−−−−−−−−−−− dodaje stronami 4b+2d=6 ⇒ 2b=3−d ⇒ 4b=6−2d podstawiam 8a+6−2d+2c+d=3 −8a+6−2d−2c+d=2 −−−−−−−−−−−−−−−−−−−−− dodaje stronami 12−4d+2d=6 −2d=−6 d=3 4b=6−2*d 4b=6−2*3 b=6−6=0 zero jest całkowite?

rumpek: magia kylo1303 ja bym skończył już na: 8b + 2d = 5 ⇔ 2(4b + d) = 5 Wniosek: po lewej parzysta, po prawej nie. Więc nieprawda

Eta:

rumpek: Dobra zostały 4 zadania, które robicie? A które robić ? Żeby się nie powtarzało.

TOmek: O OOO loooll...Jak ja nie nawidze pisać na klawie Musze miec kartke bo tak głupoty sieje ! 8a+6−2d+2c+d=3 −8a+6−2d−2c+d=2 −−−−−−−−−−−−−−−−−−−−− dodaje stronami 12−4d+2d=5 −2d=5−12 −2d=7

	7
d=−		nie należcy do ⊂ ,, pasi
	2

Eta:

TOmek: rumpek, eta jesli jest podane "o bokach długości a, b, c, i kątach α, β, γ." to ma znacznie gdzie damy kąty

rumpek: Tak α przy wierzchołku A, β przy wierzchołku B, γ przy wierzchołku C. Jak nie ma rysunku

rumpek: No i naturalnie bok b, naprzeciwko wierzchołka B, bok a przeciw wierzchołkowi A i c ...

TOmek: "naturalnie bok b, naprzeciwko wierzchołka B, bok a przeciw wierzchołkowi A i c" Pierwszy raz słysze o takim czymś i przez to źle zrobiłem zadanie....

rumpek: Zadanie 4 6sin²x + 7cosx − 1 = 0, .... x∊<0, 2π> 6(1 − cos²x) + 7cosx − 1 = 0 6 − 6cos²x + 7cosx − 1 = 0 −6cos²x + 7cosx + 5 = 0 t = cosx, t∊<−1,1> −6t² + 7t + 5 = 0 Δ_t = 49 + 120 = 169 ⇒ √Δ = 13

	−7 − 13		−20		5
t1 =		=		=		∊ Z
	−12		−12		3

	−7 + 13		6		1
t2 =		=		= −
	−12		−12		2

	1
cosx = −
	2

	2π		4π
x1 =		∨ x2 =
	3		3

kylo1303: Napisz rumpek ktore teraz zrobisz to ja tez jakies moge wziac.

rumpek: ok, za 5 minut zacznę robić zadanie 8 tylko sobie coś do picia zrobię

kylo1303: Okej, to ja sprobuje zadanie 10

Godzio: TOmek, na maturze prawdziwej wszystko będzie dokładnie określone, nie bój się

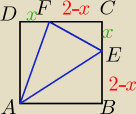
kylo1303: Pole AEF ma byc najmniejsze, wiec suma pól pozostalych trojkatow ma byc najwieksza.

	1		2x−x2
PCEF=		*x*(2−x)=
	2		2

	1
PADF=		*2*x=x
	2

	1
PABE=		*2*(2−x)=2−x
	2

	2x−x2		2x−x2		1
f(x)=PCEF+PADF+PABE=		+x+2−x=		+2=−		x2+x+2
	2		2		2

f(x) jest najwieksze w wierzcholku

	−b		−1
xw=		=		=1
	2a		−1

f(1)=2,5 Dla x=1 Pole ΔAEF jest najmniejsze.

Eta: Dokończenie .......... wyznacz to pole

Godzio: Ja chce do LO Już mam dość, przez 3 tygodnie codziennie po kilka h spędzam przed książkami ...

kylo1303: Ach, oczywiscie ze tak. Moj blad, nie chcialo mi sie popatrzec do tresci zadania (za wysoko) xD Trzeba oczywiscie odjac od pola calosci pole tego co policzylem czyli: 4−2,5=1,5 Odp. Dla x=1 i wtedy P=1,5

ZKS: Ja niestety z jednego powodu bym nie wrócił do LO (język POLSKI).

Godzio: Ja nawet to bym przeżył Nie mam życia przez tą matmę

think: Godziunia, ale jak wytrzymasz, to już za parę lat wrócisz do LO na znacząco długi okres swojego życia, więc nic nie smutaj, jeszcze będziesz tego żałował

kylo1303: Moze wybrales zly kierunek? Ewentualnie za bardzo wymagajacy. Ostatecznie mozna bylo skonczyc edukacje w liceum (badz gimnazjum) i zajac sie kopaniem dolow

Godzio: O ile się utrzymam ... jest taki natłok tego wszystkiego, że naprawdę ciężko się utrzymać, nawet mi ... Już widzę jak będą wyglądać moje wakacje z książką

TOmek: kylo1303: to samo mi wyszło

Eta: Echhh Godzio ........

Godzio: kylo prócz matmy to nic więcej nie dało by mi satysfakcji, po prostu mnóstwo roboty jest, zdecydowanie za dużo

TOmek: Godzio UWroc czy PWr?

ZKS: Dasz radę i pamiętaj co za dużo to nie zdrowo więc nie możesz się uczyć za wiele.

Godzio: PWr @ZKS, chciałem dociągnąć średnią do stypendium, ale póki co to ona systematycznie maleje

think: poradzisz sobie Godzio my w Ciebie wierzymy, zresztą najgorszy jest pierwszy rok i ostatni a reszta to czysta przyjemność

TOmek: A co dokładnie jeśli mozna wiedziec ?: D

Godzio: Na pewno ? Topologia, Teoria miary, −− to są co raz łatwiejsze przedmioty ?

Godzio: No TOmek matmę, a co innego mogę studiować

TOmek: Myślałem ,ze coś ala fiza/majma np: kierunek elektrotechnika,tam podobno we wzorach fizycznych są całki

Basiek: Rzuciłam okiem... i myślę, ze ja swoją edukację na LO chcę zakończyć. Miłego wieczoru

ZKS: Spokojnie będziesz miał średnią na stypendium.

kylo1303: Mam takie pytanko, jako ze jestem raczej laikiem w sprawach komputerowych (a jest to raczej prosta sprawa): czy nie posiadajac danych naprawczych moge naprawic rar−a ?

Mila: Godzio tylko cierpliwość i wytrwałość. Ja zwątpiłam, gdy wykładowca określił liczbę jako przekrój Dedekinda, którego nie mogłam sobie wyobrazić. Inny kazał dowodzić, że jedynka jest większa od zera, jeszcze inny dał na kolokwium wszystkie twierdzenia fałszywe. Straszą, a potem nie jest źle, studia na matematyce to najpiękniejszy okres życia. Z 200 osób przyjętych skończyło nas 60.

Godzio: No u nas jest fajniej, ze 150 przyjętych 60 już zostało

Mila: Też pięknie, pewnie załamali się. Ja sama chciałam zrezygnować, ale mama poradziła, "to może niech cię wyrzucą" i zostałam .

think: koniec użalania się nad sobą, ja tam nie widzę błędu, ale ja to ja... https://matematykaszkolna.pl/forum/140399.html

Godzio: Mnie już nie raz przeszło przez myśl zrezygnowanie, ale staram się wyrobić w sobie pracowitość i powoli mi to wychodzi, trochę za późno się obudziłem, ale nic straconego

TOmek: Tak sobie myśle jak Sam Godzio ma chwile zrezygnowania na Pwr, a ja tam chce iść... to mi sie az gorąco robi.

Godzio: A na co chcesz iść ? Nie każdy kierunek jest hardcorowy

think: Godzio... ale Ci się na zwierzenia zebrało, a ja potrzebuję wsparcia : https://matematykaszkolna.pl/forum/140399.html

TOmek: elektrotechnika/Energetyka

rumpek: Ale offtopic

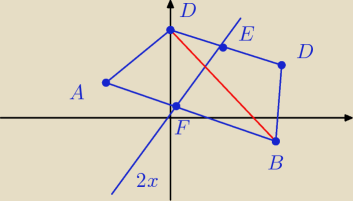
rumpek: 1^o Szukam prostej AB przechodzącej przez punkt A i prostopadłej do y = 2x

	1
y = ax + b ⇒ y= −		x + b
	2

	5		10		5		5
5 =		+ b ⇒ b =		−		⇒ b =
	2		2		2		2

	1		5
Zatem prosta AB ma postać: y = −		x +
	2		2

2^o Szukam prostej CD przechodzącej przez punkt C i prostopadłej do y = 2x

	1
y = ax + b ⇒ y= −		x + b
	2

6 = −4 + b ⇒ b = 10

	1
Zatem prosta CD ma postać: y = −		x + 10
	2

3^o Szukam punktu F.

⎧	y = 2x
⎩	y = (−1/2x) + 5/2

	1		5
2x = −		x +		/ * 2
	2		2

4x = −x + 5 5x = 5 ⇒ F(1, 2) 4^o Szukam punktu E.

⎧	y = 2x
⎩	y = (−1/2x) + 10

	1
2x = −		x + 10 / * 2
	2

4x = −x + 20 5x = 20 ⇒ E(4, 8) *********************** /////// UWAGA /////// *********************** W tym momencie można użyć wektorów, bądź |AF| = |FB|, jednak użyje innej metody *********************** a)

	x1 + x2		y1 + y2
SAB = (		,		)
	2		2

	−5 + x2		5 + y2
(1,2) = (		;		)
	2		2

x₂ = 7 y₂ = −1 B(7, −1)

	x1 + x2		y1 + y2
b) SCD = (		,		)
	2		2

	8 + x2		6 + y2
(4, 8) = (		,		)
	2		2

x₂ = 0 y₂ = 10 D(0, 10) Pozostało policzyć pole: |AB| = √(7 + 5)² + (−1 − 5)² = √144 + 36 = √180 = 6√5 |CD| = √(8 − 0)² + (6 − 0)² = √64 + 16 = √80 = 4√5 Teraz pozostało h − jest to odległość punktu C od prostej AB

	1		5
AB [		x + y −		= 0] i C = (8, 6)
	2		2

	5   |4 + 6 − |   2
h =		= 3√5
	√1/4 + 1

	a + b
P(tr) =		* h
	2

	4√5 + 6√5
P(tr) =		* 3√5 = 5√5 * 3√5 = 15 * 5 = 75 [j2]
	2

ufff 2 raz sprawdzałem obliczenia przez te ułamki

rumpek: Dobra zostało ostanie

Godzio: Tomek to tam jest lajcik

TOmek: uffff ,,mam nadzieje

TOmek: chyba ,ze to był sarkazm, ale wole sobie wmówic ,ze nie

Eta: h= |EF|= ..... =3√5

rumpek: 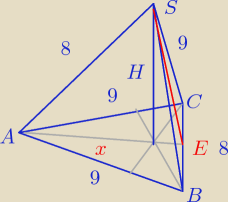Zadanie 12 1^o P_p − trójkąt równoramienny, bo |AB| = |AC| = 9 h² + 4² = 9² h² + 16 = 81 h² = 65, h∊R₊ h = √65

	1
Pp =		* a * h
	2

P_p = 4 * √65 2^o Szukam wysokości Rozpatrzmy trójkąt △BSC, jest on równoramienny więc obliczyć długość |SE| nie jest problem Dokładnie taka sama jak w podstawie, zatem trójkąty są przystające. * 8² = H² + x² ** (√65 − x)² + H² = √65)² * H² = 64 − x² ** 65 − 2√65x + x² + 64 − x² = 65

	32√65
** −2√65x = −64 ⇔ x =
	65

Zatem wysokość ostrosłupa to:

	1024 * 65		270400
H2 = 64 − (		) =		− U{66560} =
	4225		4225

	203840		3136
=		=		, H∊R+
	4225		65

	56		56√65
H =		=
	√65		65

3^o Pozostała objętość:

	1
V =		* Pp * H
	3

	1		56		224		2
V =		* 4 * √65		=		= 74		[j3]
	3		√65		3		3

ufff

rumpek:

kylo1303: Takie troche gowniane liczby

Godzio: Żeś się napracował

rumpek: niestety żeby takich na właściwej nie było

kylo1303: No wlasnie. Najgorsze w takich liczbach jest to ze nie masz pewnosci czy sie nie pomyliles. Czasami wystarczy zly znak, nie dodasz jedynki czy cokolwiek i potem wez szukaj bledu... Pozostaje miec nadzieje ze takich zadan nie dadza.

rumpek: Najgorzej było z analityczną tymi ułamkami

kylo1303: Taaa, dlatego ja sie nie zabieralem za pisanie rozwiazania na forum. Zbyt duzo roboty. Takie pytanie do maturzystow: chodzicie jeszcze do szkoly? I nie chodzi mi czy macie lekcje bo kazdy ma, chodzi mi o wasze indywidualne podejscie.

rumpek: Nie chodzę do szkoły, w czwartek rada. Na lekcjach nic nie powtarzamy − na matematyce tylko arkusze do robienia, polski coś tam z "Tanga" Mrożka. Więc wychodzę z założenia, że wolę pracować w domu bo więcej powtórzę niż na bardzo luźnych lekcjach. Po prostu się nie opłaca chodzić do szkoły już

kylo1303: Czyli nie jestem jedyny. Chociaz u mnei to roznie bywa z tym "przygotowywaniem w domu". Czasami pojde na lekcje i zrobie tam wiecej niz w domu, gdzie wstane po 12, do tego majac dostep do komputera, telewizora i lodowki− czas na zadania jest bardzo ograniczony. Wiesz moze do kiedy mozna zmieniac bibliografie?

rumpek: Można zmieniać? Ja już nie mogę miałem oddać ostateczną do 02 kwietnia to była tragiczna data

Basiek: <wtrąca się> U mnie do środy

rumpek: Tak za pamięci * w czerwcu była "Nie−Boska Komedia" * w sierpniu była "Lalka" co obstawiacie teraz w maju z polskiego?

Basiek: Dziady

rumpek: mogą być ostatnio czytałem streszczenie. Ale były 2 lata temu − nie będzie

kylo1303: Tzn oddac trzeba bylo jzu wczesniej, ale zmieniac podobno mozna do jakiegos terminu. A ja nawciskalem na sile do literatury przedmiotu, a potem slucham od nauczycielki "nie powinno sie wstawiac opracowan z ktorych sie nie korzystalo"... I musze wyrzucic 2 rzeczy. A tak zebyscie sie nie nudzili to wrzuce zadanka, ktore juz dawalem ale nikt nie dal poki co odpowiedzi: 1. Jakie trzy parami różna liczby całkowite względnie pierwsze mogą być pierwszymi trzema wyrazami ciągu arytmetycznego i jednocześnie (w innym porzadku) pierwszymi trzema wyrazami ciagu geometrycznego. 2. x(y+z)=1 y(x+z)=1 z(y+x)=p Przedyskutuj liczbe rozwiazan w zaleznosci od parametru p. 3.f(x)=x²−4|x−1|−p Znajdz p, dla ktorych funkcja f(x)=1 ma dokladnie 3 różne rozwiazania. Zadania z konkursu, jakies tam wyniki mialem ale drugi raz robic mi sie nie chce Moze ktos sie pokusi

Eta: No to......... dwa w jednym → "Boska Lalka "

rumpek:

Eta:

rumpek: Osobiście obstawiam Szymborską i Przedwiośnie lub Pan Tadeusz lub Chłopi lub Zbrodnia i Kara. Na pewno w coś trafię

Basiek: Dziady mnie prześladują. Z moim szczęściem, będą. Jutro mam spr. z całej młodej polski. Co ja robię?... Co do karty prezentacji− dziś mi nauczycielka poprawiła i odesłała mailem. W każdej szkole sprawa tych kart jest dość.... indywidualna. Nauczyciele się zwyczajnie tym wymieniają, tu sobie ustalą "jeszcze kilka dni" itd. No i ... da się. Btw. wydaje mi się, że zawsze można udać się do sekretariatu i tam "drogą bardziej oficjalną" to poprawić. Przynajmniej jeśli jeszcze "nie poszły w świat"

rumpek: U mnie "poszły w świat" przed świętami Dlatego już napisałem cały wstęp − dokładnie 198 słów

Basiek: Ech. Wow. Miałeś mi dać znać! Teraz też muszę zacząć... pisać

rumpek: Spokojnie nie określiłem kiedy skończę

Basiek: Ja ostatnio (od tygodnia) nic nie robię, bo odczuwam jakieś takie... koszmarne zniechęcenie. A dziś zapisałam się na konkurs i stwierdziłam, że maturę ... olewam, bo nie mam ochoty. Ale pracę napiszę...

rumpek: Basiek ty w ogóle chodzisz jeszcze do szkoły ?

Basiek: Oczywiście. Jutro spr. z matematyki + spr. z polskiego z całej Młodej Polski+ Tango

rumpek: Sprawdzian? Do jakiej szkoły ty chodzisz ja się pytam Czy ci nauczyciele nie mają ciekawszych zajęć No chyba, że jesteś 2 klasie

Basiek: Nie, uwierz mi, że nie mają ciekawszych zajęć. Sama się zastanawiam, dlaczego a) chodzę do takiej szkoły (chyba była najbliżej) b) ja jeszcze do niej chodzę c) nie mam wystawionych ocen jeszcze?! d) nikt nie przygotowuje mnie do matury. Błądzę w ciemności.

rumpek: my Ciebie przygotowujemy

Basiek: A tak serio.... naprawdę już sobie tę maturę 2013 planuję. Co do matematyki... jutro sprawdzian (kolejny), a ja po prostu NIC nie umiem Chyba pójdę się nauczyć

Godzio: Pisz przez komórkę na forum, ktoś Ci go rozwiąże

rumpek: Z czego ?

rumpek: Ostrosłupy?

Basiek: Hahaha <3 Uwielbiam Was. Optymalizacja w stereometrii. Zadania najpewniej będą z bryły wpisanej w inną bryłę. Coś na podstawie Kiełbasy Pół klasy ocena łamana, ale oczywiście ja musiałam z tego w piątek 13−tego odpowiadać.

rumpek: Chorą masz nauczycielkę już wolne być powinno W zasadzie i tak nie będę chodził przez cały tydzień będę miał czas na zrobienie ciekawszych dowodów

Basiek: Nawet nie chcę już o niej źle mówić. Wszyscy chcą ją przez okno wyrzucić lub coś w tym stylu. Z 5/6 osób ma zagrożenie z matmy. Zamiast im to popoprawiać, czy coś...., to w sumie nie wiem, co ona robi. Pyta innych, sprawdzianów robi masę, maturę naszą olała, bo stwierdziła, ze to nasz problem...

rumpek: Proste − Nie miała dzieciństwa

Basiek: Dopiszę ją do mojej pracy maturalnej

rumpek: A co masz taki temat? "Wiedźmy w polskiej literaturze." ?

Basiek: Temat: Przedstaw funkcjonowanie motywu dziecka w literaturze i malarstwie. TEZA: Wizerunek dziecka w sztuce jest różnie prezentowany a)potwiedzenie archetypu dziecka w sztuce: b)DEMITOLOGIZACJA dzieciństwa i dziecka w tekstach literackich: Pasowałaby do b.

rumpek: a jak tam Basiek robisz jakieś dowody z matmy ?

Basiek: rumpek melduję Ci, ze od tygodnia nie zrobiłam NIC. Z niczego. Mam fazę wyparcia. A ja nigdy nie robię nic na pół gwizdka. Stwierdziłam, ze matura mnie nie dotyczy.

rumpek: spokojnie − dasz stówkę na tacę i maturkę się załatwi

Basiek: No raczej nie. Ja to w tym roku do Częstochowy poszłam na nogach o cud prosić Ale nie wyszło...

rumpek: zdasz Pomyśl sobie, że taka twoja Pani od matmy zdała to ty też zdasz

Basiek: Ona miała legendarnego nauczyciela od matmy Wkogośtam. No i jest po biolchemie. Ale naprawdę wszyscy się głowimy, jak ona to zdała "Eeeeee.... gdzie? Co? Aaaa, tu. No nie wiem, musiałabym to sprawdzić. <szybka zmiana tematu>"

rumpek: ja tak mam na fiz podchodzi do tablicy i mówi "jeden plus jeden, zgadza się;siadaj" 1 zadanie na całą lekcję

Basiek: To wiesz, co to znaczy. Jesteśmy jej pierwszym rozszerzeniem. Więc ... eksperyment się nie powiódł A z fizyki to gościu jest genialny. Nie dość, ze wszystko wie, coś tam całkuje, tu pochodna, tam do potęgi kappa ... Fajna sprawa. Szkoda, że nie jestem zainteresowana fizyką

rumpek: spokojnie wszystko z czasem

rumpek: Ooo "Killer" leci w telewizji To będę leciał Przyjdę tak jeszcze koło 2 Powodzenia jutro na sprawdzianie

Basiek: Jak się na niego wybiorę... Dobranoc Nocny Marku

max: rumpek lub ktoś mógłby zrobić zadanie 9 tym sposobem z podobieństwa trójkątów?