Proszę o pomoc WAS WASZYSTKICH Fifi: Z punktu A (−9,12) poprowadzono styczne do okręgu o równaniu x²−12x+y²+16y=25. Oblicz długość odcinka łączącego punkty styczności.

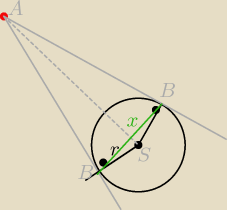
think: równanie okręgu: (x − 6)² + (y + 8)² = 125 S = (6, −8) r = 5√5 skorzystam z pola trójkąta ABS, ponieważ to jest trójkąt prostokątny. |AS| = √(6 + 9)² + (−8 − 12)² = √225 + 400 = 25 z tw. Pitagorasa liczę |AB| |AB|² = 25² − (5√5)² = 625 − 125 = 500 |AB| = 10√5

	1		1
pole |ABS| =		*r*|AB| =		*5√5*10√5 = 125
	2		2

	1		x
ale pole |ABS| również =		*		*|AS|
	2		2

	x
125 =		*25 ⇒ x = ...
	4

Fifi: czyli x to będzie już końcowy wynik?