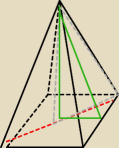
. Kuba: Zadanie proste,ale sie motam troche,gdzies robie błąd. Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 10√2 . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 45∘ . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa. d=a√2 10√2=a{2}//√2 a=10 Pp=a² Pp=100 z tego "siwego trójkąta" obliczyłem H( kąt 45 stopni)tg 45=^H_5√2 z proporcji wyszło że H=5√2 Obliczyłem hb(wyskosc sciany bocznej z pitagorasa,ten zielony trójkąt) Gdzie: hb²=(5√2)²+(5{2})² <−− wysokosc i pół długosci przekątnej hb=10. podstaiwłem pod wzór,ale wynik sie nie zgadza z podanym w książce.. Gdzie robie błąd

tim: Jest ok. P_b = P_p + 4P_ś = 100 + 4 * 50 = 300

tim: Taka jest odp?

dpelczar: Dobrze jest

dpelczar: Tim pomoż mi z zadaniem wrzuciłem własnie na forum... z ciągiem arytmetycznym

tim: dpelczar, widziałem, ale ciągi to nie moja dziedzina [ze względu na mój wiek]

dpelczar: aha no to ok − dzieki A nie wiesz kto tutaj moze takie cosik zrobic? Bo widzialem podobne zadania ale dla parzystych indeksow... a z tym nie mam szans sobie poradzic...

tim: Bogdan może pomoże

dpelczar: hmmm tylko gdzie go złapac

Kuba: znalazłem rozwiązanie na zadania.info http://www.zadania.info/d42/4643983 i sie nie zgadza...

Kuba: co Ty na to tim? ...

tim: Teraz widzę błąd , policzyliśmy złego Pitagorasa, powinno być H² + (1/2 a)² = h_b²

Kuba: czyli pod A powinno znajdowac sie 10 czy połowa tej przekątnej?

tim: Na rysunku widać, że ten odcinek zielony na podstawie to połowa oku

Kuba: echh,,no właśnie,ok dzięki tim!byc może jeszcze tutaj przybęde z kolejnym zadaniem..xD