 Metoda "osi i tabelki":
|x2+6x−7|>6+|x+7|
Liczę miejsca zerowe obu modułów:
1) Δ=62−4*1*(−7)=64, √Δ=8
x1=−7, x2=1
2) x=−7
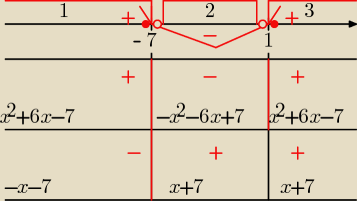
1o x2+6x−7>6−x−7, dla x≤−7
2o −x2−6x+7>6+x+7, dla x∊(−7, 1)
3o x2+6x−7>6+x+7, dla x≥1
Rozwiąż te 3 nierówności, wyznacz części wspólne tych nierówności z założeniami dla
poszczególnych przypadków, a potem zsumuj rozwiązania 1oU2oU30.
Metoda "osi i tabelki":
|x2+6x−7|>6+|x+7|
Liczę miejsca zerowe obu modułów:
1) Δ=62−4*1*(−7)=64, √Δ=8
x1=−7, x2=1
2) x=−7
1o x2+6x−7>6−x−7, dla x≤−7
2o −x2−6x+7>6+x+7, dla x∊(−7, 1)
3o x2+6x−7>6+x+7, dla x≥1
Rozwiąż te 3 nierówności, wyznacz części wspólne tych nierówności z założeniami dla
poszczególnych przypadków, a potem zsumuj rozwiązania 1oU2oU30.