Oblicz Marek:

	1
A i B są takimi zdarzeniami zawartymi w Ω, że P(A\B)=P(B\A)=		i P(A'uB')=1
	7

Oblicz P(A'nB')

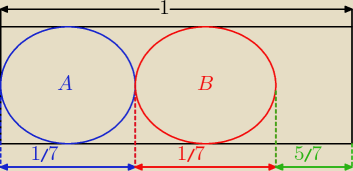Gustlik: Z praw de Morgana mamy: A'UB'=(A∩B)', stąd P(A'UB')=P(A∩B)'=1−P(A∩B)⇒P(A∩B)=0, zdarzenia A i B wykluczają się. P(A'∩B')=P(AUB)'=1−P(AUB) z drugiego prawa de Morgana

	1		1		2
P(AUB)=		+		=		− widać to z rysunku
	7		7		7

	5
zatem P(A'∩B')=P(AUB)'=1−P(AUB)=
	7