PILNE Aga:

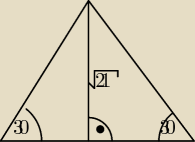
	√1323
Oblicz pole wyszło mi takie coś i chyba to jest źle P=
	9

maturzysta: ale dlaczego podzieliłaś przez 9 ?

Saizou : postawa ma wzór 2a√3, gdzie a=√21 zatem 2*√21*√3

	√21*2*√21*√3		42√3
Pole=		=		=21√3
	3		2

tak mi się wydaje ale jest późno i mogę robić błędy

asdf: dobrze przepisałaś odp? 2x = a

	√21
tg30o =
	x

√3		√21
	=
3		x

3√21 = x√3 3√21 * √3 = 3x 3√63 = 3x x = √63

	√63
a =
	2

	1
P = a * h *
	2

	√63		√21
P =		*
	2		2

	√1323
P =
	4

Saizou : ale jeśli założyłeś że 2x=a to a=2√63 tak by wynikało z twoich obliczeń

asdf:

	21√3
lub: P=
	4

asdf: @Saizou Masz racje więc P = √1323 = 21√3

Saizou : to jeszcze coś kontaktuję

Saizou : a nie łatwiej byłoby z zależności w trójkącie 30,60,90

Aga: już wiem, co robilam źle, dzięki

asdf: Saizou, nie znam wzoru na pole trójkąta kątów 30,60,90

mala: z własności trójkatów o katach 90, 60, 30 st. h = √21 1/2a = √21 a = 2√21 P =^ah₂ w mianowniku 2 zamiast 3, pewnie Aga zauważyła.

Saizou :

	ab
a powiem ci że nasz p=		, bo jest to trójkąt prostokątny, a swoją drogą to tylko
	2

potrzepujesz własności żeby obliczyć połowę podstawy w trójkącie na rysunku

Saizou : *znasz

asdf: Nie bardzo rozumiem mala, według mnie to on(a) obliczyła przeciwprostokątną, a nie bok a