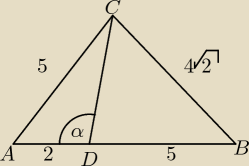
PILNE Baśka: Oblicz sinα

rumpek: Kąt |∡ADC| = α, zatem kąt |∡BDC| = 180^o − α Stosuję teraz tw. cosinusów: |CD| = x 1^o 5² = 2² + x² − 2 * 2 * x * cosα 2^o (4√2)² = 5² + x² − 2 * 5 * x * cos(180^o − α) [ cos(180^o − α) = −cosα ] 1^o 25 = 4 + x² − 4xcosα 21 − x² = −4xcosα / : −4x , bo x > 0

	x2 − 21
cosα =
	4x

2^o 32 = 25 + x² + 10xcosα

	x2 − 21
7 = x2 + 10x *
	4x

	10x2 − 210
7 = x2 +		/ * 4
	4

28 = 4x² + 10x² − 210 14x² − 238 = / : 14 x² − 17 = 0 (x − √17)(x + √17) = 0 x = √17

	x2 − 21
Podstawiasz teraz pod cosα =		, jak będziesz miała wyliczone cosα pozostanie
	4x

skorzystać z sin²α + cos²α = 1

filip: zastosuj twierdzenie cosinusów dla obydwu trójkątów i będziesz miała dwa równania, z których wyliczysz cosα. jakby co to cos(180−α)=cosα a później zamień cosinus na sinus

Basia: oblicz pole trójkąta P np. z wzoru Herona potem wyznacz sin(∡A) z równania

	1
P =		*7*5*sin(∡A)
	2

no a potem twierdzenie sinusów −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− albo: (moim zdaniem łatwiej) liczymy cos(∡A) z tw.cosinusów sin(∡A) z jedynki trygonometrycznej sinα z tw.sinusów