liniowa Tomek: Dany jest prostokąt o wierzchołkach A(3;2) B(0;2) C(0;−4) D(3;−4) oraz prosta k o równaniu y=mx−m, gdzie m jest parametrem. Uzasadnij, że istnieją punkty na brzegu prostokąta, przez które nie przechodzi żadna prosta określona równaniem tej prostej.

Basia: Podpowiadam

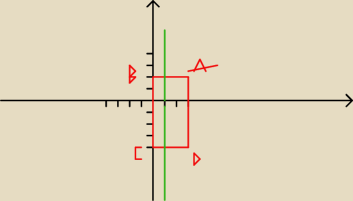
Basia: y = mx−m = m(x−1) dla m=0 mamy prostą y =0 i ona na pewno nie przechodzi przez punkty M(1,2)∈odc.AB i N(1,−4)∈odc.CD dla m≠0 m(x−1) = 0 ⇔ x−1=0 ⇔ x =1 prosta przecina oś OX w punkcie 1 gdyby ta prosta przechodziła przez M lub N musiałaby mieć równanie y =1 a to jest niemożliwe bo m≠0 wniosek: żadna prosta o równaniu y = mx+m nie przechodzi ani przez M ani przez N

MATURZYSTA: Możesz mi wytłumaczyć czemu y=0 niemoże być, przecież przecina bok BC i AD w tym samym punkcie y A w drugim czemu m(x−1) porównałaś do 0

MATURZYSTA: Też próbowałem rozwiązać, ale także niewiem jak