 No to jeszcze jedno zadanie konkursowe
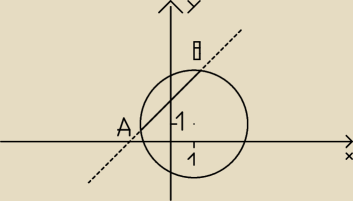
No to jeszcze jedno zadanie konkursowe  Napisz równanie okręgu o środku S=(1;1), który na prostej o równaniu x − y + 4 = 0 odcina
cięciwę AB długości 2√2. wykonaj odpowiedni rysunek.
Napisz równanie okręgu o środku S=(1;1), który na prostej o równaniu x − y + 4 = 0 odcina
cięciwę AB długości 2√2. wykonaj odpowiedni rysunek.
 Dzień dobry.
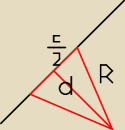
R długość promienia okręgu
c = 2√2 − długość cięciwy
d − odległość punktu S(1, 1) od prostej x − y + 4 = 0
Dzień dobry.
R długość promienia okręgu
c = 2√2 − długość cięciwy
d − odległość punktu S(1, 1) od prostej x − y + 4 = 0
| |1*1 − 1*1 + 4| | 4 | |||
d = | = | = 2√2
| ||
| √11 + 11 | √2 |