Zadanie matura MATURZYSTA: Proszę o pomoc w tych zadaniach: Zadanie 1. Dane sa odcinki o długosciach a = 2x +1, b = 3 − y , c = x + 2y . Opisz za pomoca układu nierównosci zbiór tych wszystkich punktów (x, y ), dla których z odcinków o długosciach a, b, i c można zbudowac trójkat. Zaznacz ten zbiór w układzie współrzednych. Czy punkt A(3, 1) spełnia ten warunek? Zadanie 2. Dla jakich wartosci parametru p iloczyn zbiorów A i B jest zbiorem pustym, jeżeli A = {(x, y): x R i y  R i x² + y² − 6x ≤ 2y + 8 ≤ 0} B = {(x, y): x R i y  R i x − y + p < 0}. Dla najmniejszej znalezionej wartosci parametru p przedstaw interpretacje geometryczna. Zadanie 3. Wielomian W(x) przy dzieleniu przez x −1, x − 2, x − 3 daje odpowiednio reszty 1, 2, 3. Wyznacz reszte z dzielenia wielomianu W(x) przez iloczyn (x −1)(x − 2)(x − 3) . Zadanie 4. Reszta z dzielenia wielomianu W(x) przez wielomian Q okreslony wzorem Q(x)=x⁴+x³−x−1 wynosi x³+x²+x+2. Wyznacz reszte z dzielenia wielomianu W(x) przez x²−1 . Zadanie 5. Rzucono trzy razy kostką. Oblicz prawdopodobieństwo tego, że wylosowane liczby tworzą ciąg arytmetyczny. Zadanie 6. W urnie znajduje się 10 kul czarnych, ponumerowanych od 1 do 10 oraz 10 kul białych również ponumerowanych od 1 do 10. Losujemy dwie kule. Co jest bardziej prawdopodobne wylosowanie kul o różnych kolorach, czy o różnych numerach? Zadanie 7. Dany jest zbiór W wielomianów postaci ax² + bx +c , gdzie współczynnik a, b, c przyjmują wartości ze zbioru {−1,0,1} oraz a≠0. Obliczyć prawdopodobieństwo, że losowo wybrany wielomian ze zbioru W jest podzielny przez (x−1). Zadanie 8. Dany jest zbiór wszystkich funkcji f: {1,2,3} → {1,2,3,4,5}. Obliczyć prawdopodobieństwo tego, ze losowo wybrana funkcja z tego zbioru będzie różnowartościowa. Zadanie 9. Wybieramy losowo trzy różne liczby naturalne ze zbioru {1,2,3...,99,100}. Czy bardziej prawdopodobne jest wybranie trzech liczb podzielnych przez 4, czy wybranie trzech liczb z których można utworzyć ciąg arytmetyczny? Zadanie 10. Dla jakich wartości parametru m równanie (m +1)×9^x − 4m× 3^x + m +1 ma dwa rozwiązania?

tim: Pomogę I.

tim: a = 2x +1, b = 3 − y , c = x + 2y Żeby powstał trójkąt musi być spełniony warunek: a + b > c a + c > b b + c > a 2x + 1 + 3 − y > x + 2y 2x + 1 + x + 2y > 3 − y 3 − y + x + 2y > 2x + 1 Po przekształceniach. x + 4 > 3y 3x + 3y > 2 y + 2 > x Przerzucamy. y > x − 2

	2
y > −x +
	3

	1		4
y <		x +
	3		3

Rysujesz układ współrzędnych. Zaznaczasz trzy funkcje oraz obszary: y = x − 2 [nad nią]

	2
y = −x +		[nad nią]
	3

	1		4
y =		x +		[pod nią]
	3		3

Powstaje trójkąt, a część wspólna spełnia warunki. Aby sprawdzić, czy punkt A spełnia warunek mozesz odczytać z rysunku, ale trzeba sprawdzić. y > x − 2

	2
y > −x +
	3

	1		4
y <		x +
	3		3

Do układu równań wyżej wstawiasz x = 3, oraZ y = 1. Sprawdzasz i wychodzi Pozdrawiam

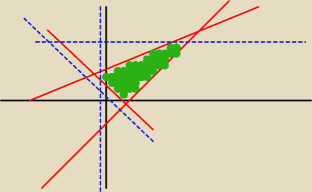
tim: Po przemyśkleniu jeszcze trzeba pamiętać, że boki nie mogą być ujemne, więctrzeba zrobić założenie. 2x + 1 > 0 3 − y > 0 x + 2y > 0 Wynika: x > −0,5 y < 3 y > −0,5x Po narysowaniu wynika, że obszar jeszcze się pomniejsza. Rysunek pomocniczy − nie przerysowywać. Czerwone − ograniczniki a + b >c, niebieskie ograniczniki dodatnie. Wspólny obszar niebieskich i czerwonych spełnia wymagania. Uwaga! Punkty na liniach nie należą do wymagań.

tim: Bogdan spr.

Bogdan: Cześć tim, zaraz sprawdzę

tim: Ok. Po dokładnijszym narysowaniu wnioskuję, że założenia 2x + 1 >0 itd. nie mają większego znaczenia do tego zadania, ale należy je zapisać..

kłopoteq: Geniusze matematyczni z Was

tim: Ja dopiero raczkuje

kłopoteq: Tia jasne a wszystkie zadania robi i niby raczkuje

Bogdan: tim − dobrze rozwiązałeś

tim: Dziękuje. A to założenie potrzebne?

dpelczar: Eeee TIM i Bogdan... nie zrobil bym tego zadania... − a tak apropo to zaczynam na tym forum do piero... a w tym roku pisze mature z matemantyki rozszerzonej... jak byście mieli jakies fajne zadania maturalne to podrzuccie gdzies − chetnie porobie a jak nie dam sobie rady to prosiłbym was o pomoc...

tim: dpelczar, to weź się do nauki porządnie Są na tej stronie, z poprzednich lat i próbne , wraz z rozwiązaniami PS. kłopoteq − raczkuje, dopiero 14

Bogdan: Proponuję stronę http://www.zadania.info/

dpelczar: O dziekuje A nie wiesz czasem jak by zrobic zadanie z ciągów... nie poradze sobie z nim... dalem na forum...

Bogdan: Wiem, zadałem Ci tam pytanie.

Mickej : (m +1)9^x − 4m3^x+m+1=0 nie ma równań wykładniczych na maturze ale zróbmy t=3^x t>0 (m+1)t²−4mt+m+1=0 no i teraz rozwiązać takie założenia 1.Δ≥0 2. t₁t₂>0 t₁+t₂>0

Mickej : z tymi zbiorami zadanie 2 dobrze przepisałeś zbiór A

Mickej : zadanie 3 skorzystaj z tego W(x)=P(x)Q(x)+R(x) gdzie W(x) nasz wielomian który przy dzieleniu przez 1,2,3 daje nam odpowiednie reszty P(x) wielomian przez który dzielimy i 1,2,3 to jego miejsca zerowe więc sie nam zeruje Q(x) wielomian powstały w wyniku dzielenia ale on sie z zeruje po pomnożeniu z P(x) R(x)= ax²+bx+c reszta z dzielenia pierwsze równanie to bedzie W(1)=(x−1)(x−2)(x−3)Q(1)+a*1²+b*1+c czyli 1=a+b+c tak samo dla 2 i 3 bedziesz miał 3 układy równań i 3 niewiadome dasz rady

Mickej : Jeżeli zbiory przepisałeś dobrze to dla p≥3+3√2

MATURZYSTA: Dziękuje wszystkim za pomoc, Mickiej ten zbiór jest edobrze przepisany. Prosiłby jeszcze o podpowiedzi do zadań z prawdopodobieństwami, bo z tym mam największy problem.

Mickej : z kośćmi wszystkich możliwości mamy Ω=6³ a takich które tworzą ciąg to nie da sie inaczej niż rozpisać 111 222 333 444 555 666 123 234 345 456 135 246 no i tyle by było z zadania bo dalej już wiesz

Mickej : a no jeszcze sory bo mogą być malejące przecież jeszcze

MATURZYSTA: Mickiej zbiór A ma być A = {(x, y): x R i y  R i x2 + y2 − 6x ≤ − (2y + 8 ) ≤ 0}. Mam prośbę mógłbyś wytłumaczyć jak to zrobiłeś, bo ja dochodzę do stycznej z okręgiem, ale wychodzą mi 2 wynik Proszę o podpowiedź

Mickej : ale masz mniejsze bądź równe czyli jedna styczna automatycznie odpada ta z góry

MATURZYSTA: Mickiej niesądzisz, że w zadaniu 3 jest błąd w treści? Bo po wyliczeniu wychodzi mi c=0, a następnie a=0, ale podkładając do innego równania to samo a wychodzi 2 Proszę kogokolwiek o radę czy przemyślenia.

MATURZYSTA: nie, ta prosta jest większa y>x+p więc odpada ta z dołu, ale chodzi mi czy mam to jakoś wyliczyć, czy mógłbym to poprostu tylko napisać

Mickej : ja wpisuje kwadrat w koło i wyliczam ale da sie też z odległości prostej od punktu czyli środka okręgu a co do 3 nie wiem nie sprawdzałem

Mickej : sprawdze teraz

MATURZYSTA: acha, a mógłbym mi powiedzieć ( jeśli wiesz ) w zadaniu 4 w odp. jest napisane, że trzeba "Zauważamy, że reszta z dzielenia W przez x²−1 jest równa reszcie z dzielenia x³+x²+x+2 przez x²−1". Mógłby mi ktoś to wyjaśnić bo naprawdę nierozumiem tego stwierdzenia.

Mickej : no w tym 3 jest coś pokićkane a co do twojego pytania to nie wiem wróciłem o 6 do domu to jestem jeszcze trochę zmięty ale zaraz sie odświeżę i możn to zrozumiem

MATURZYSTA: ok, wielkie dzięki i tak