funkcje wielomianowe demoo: Po naszkicowaniu odpowiednich wykresów określ, ile rozwiązań ma równanie −x¹⁰⁰−x²+1=0. proszę o wytłumacznie

MQ: x¹⁰⁰ to taka "parabola" "spotęgowana" 50 razy, więc zachowuje się jak x² czyli −x¹⁰⁰ będzie zachowywać się jak −x² Ich suma będzie prawie tak wygladać jak −x¹⁰⁰ a poniważ masz +1 więc wykres będzie wyglądać jak baaaaaaardzo wydłużona parabola −x² podniesiona o +1, czyli będzie oś OX przecinac w 2 punktach, więc masz dwa rozwiązania.

demoo: nie wiem czy mogę ale jakbym to rozbił na coś takiego −x¹⁰⁰=x²−1 x=0 v x=1 v x=−1

AS: f(x) = −x¹⁰⁰ − x² + 1 = 0 Wyznaczam pochodną f(x) f '(x) = −100*x⁹⁹ − 2*x = −x*(100*x⁹⁸ + 2) Pochodna f'(x) = 0 dla x = 0 Dla x < 0 f'(x) > 0 a dla x > 0 f'(x) < 0 oznacza to,że dla x = 0 istnieje maksimum a więc krzywa musi dwukrotnie przeciąć oś Ox. Stąd musi posiadać dwa rozwiązania i tylko dwa.

Grześ: dobra, określiłeś ekstremum w punkcie x=0... a jaka jest wartość funkcji w tym punkcie, hę?

Grześ: uzasadnij dokładnie... oczywiście masz racje... ale dokładniej wytłumacz im to

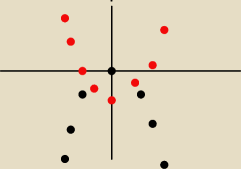
AS: Graficznie. Rozpisuję na dwie funkcje f(x) = −x¹⁰⁰ i f(x) = x² − 1 Wykresy wyjaśniają wszystko.

AS: Ojej − no to podstaw do równania funkcji f(0) = −0¹⁰⁰ − 0² + 1 = 1