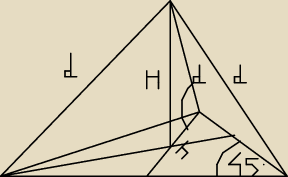
oblicz objętoś ostrotosłupa imię lub nick: Witam, mam zadanie z konkursu matematycznego pod patronatem Instytutu Matematyki Wydziału Matematyczno − Fizycznego Politechniki Śląskiej dla uczniów szkół ponadgimnazjalnych. Podstawą ostrosłupa jest równoramienny trójkąt prostokątny. każda krawędź boczna ma długość d i jest nachylona do płaszczyzny podstawy pod kątem α. Oblicz objętość ostrosłupa. Dane: d i α (nieopisany kąt na rysunku to kąt α)

	H
sinα=		⇒ H=dsinα
	d

ale nie wiem jak przedstawić krawędź podstawy za pomocą d i α.

gim:

	d3cos2α*sinα
Odp: V =
	3

Basia: niech a − przyprostokątna wyraź h przy pomocy a wyraż r (promień okregu wpisanego w podstawę) przy pomocy a

	h−r
sinα =
	d

to Ci da zależność między a i d

Basia:

	h−r
cosα =		oczywiście (nie sinus)
	d

	H
sinα=
	d

wynik się zgadza

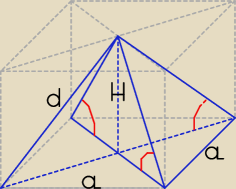
Bogdan: Może ten rysunek ułatwi zrozumienie treści zadania. Widzimy, że podany w zadaniu ostrosłup to część graniastosłupa prawidłowego czworokątnego o krawędzi podstawy a. Krawędzie boczne nachylone są do płaszczyzny podstawy pod kątemα (kolor czerwony). Wysokość graniastosłupa i ostrosłupa ma długość H.

tim: Piękny rysunek Bogdan

Bogdan: Dziękuję tim, rysowałem trochę z nudów, bo mało zadań jest dzisiaj.

Basia: Bogdanie rysunek piękny, ale jeżeli wszystkie krawędzie boczne są nachylone do pł.podstawy pod tym samym kątem to spodek wysokości jest środkiem okręgu wpisanego w podstawę. To nie jest ostrosłup z Twojego rysunku.

Bogdan: Czy widać na moim rysunku, że wszystkie krawędzie boczne ostrosłupa mają tę samą długość d i że są nachylone do płaszyznay podstawy pod tym samym kątem α?

Eta: Basia! masz 100% racjii spodek wysokości H jest środkiem przeciwprostokątnej! H −−−− leży w scianie ,ktorej podstawą jest przeciwprostokatna! gim to ............. zgadnij ? Tak mi wyszło z obliczeń

Eta: Bogdanie, piękny rysunek Widzę na nim to co brałam pod uwagę rozwiązując to zadanie! Jeszcze mogłeś oznaczyć wierzchołki ostrosłupa wówczas byłoby wszystko zauważalne!

Bogdan: Nie ma co za bardzo dzisiaj robić, więc zachęcam do kontynuowania tej rozmowy. Będę drążył dalej. W którym miejscu rysunku jest niezgodność z treścią zadania, zapraszam szczególnie tegorocznych maturzystów do wypowiedzi.

Basia: ale poza tym wszystko się zgadza; czyli mogą chyba być dwa różne rozwiązania

Basia: Nie chyba, na pewno.

Karola: Kazda krawedz boczna ma byc nachylona pod tym samaym katem do plaszczyzny podstawy − na twoim rysunku jest to niemozliwe poniewaz wysokosc ostroslupa jest jednoczenie wysokoscia jednej ze scian bocznych.

Eta: Ja widzę na Twoim rysunku cztery przystające ostrosłupy z których każdy spełnia w_k zadania! Czy tak?.........

Basia: Mam dziś zły dzień. Oczywiście Bogdanie masz 200% racji.

Bogdan: Do Karoli. Weźmy jeszcze raz treść zadania: Podstawą ostrosłupa jest równoramienny trójkąt prostokątny. Na rysunku podstawą ostrosłupa jest trójkąt prostokatny równoramienny. Każda krawędź boczna ma długość d Na rysunku każda krawędź boczna ma jeden koniec w wierzchołku prawidłowego graniastosłupa, a drugi koniec w środku górnej podstawy graniastosłupa, a więc krawędzie boczne są równe. i jest nachylona do płaszczyzny podstawy pod kątem α. Ten warunek jest również spełniony. Karolo, co dokładnie wg Ciebie jest niemożliwe?

Eta: Bogdan! ........ ja czekam na odpowiedź na moje pytanie? czy dobrze widzę te ostrosłupy?

Bogdan: Podam więc twierdzenie, które powinno być przydatne szczególnie maturzystom. Jeśli wszystkie krawędzie boczne ostrosłupa są równe lub jeśli wszystkie krawędzie boczne tworzą z płaszczyzną podstawy równe kąty, to na podstawie ostrosłupa można opisać okrąg, a środkiem tego okręgu jest spodek wysokości ostrosłupa. W tym zadania zachodzą jednocześnie te dwa warunki.

Bogdan: Tak Eto, w tym graniastosłupie jest więcej takich ostrosłupów. W zwiazku z tym 2 pytania: 1. Jeśli odwrócimy ten graniastosłup "do góry nogami", to ile będzie wszystkich takich ostrosłupów spełniających warunki zadania? 2. Czy wszystkie te ostrosłupy są do siebie przystające, czyli czy są identyczne?

Basia: Na kazdej z podstaw można zbudować takie 4. Razem 8. Są przystajace. Dobrze widzę ? Bo na prawdę mam dziś zły dzień.

Bogdan: I drugie zwiazane z omawiamym tematem twierdzenie: Jeśli wszystkie ściany boczne ostrosłupa tworzą z podstawą równe kąty lub jeśli wysokości wszystkich ścian bocznych, poprowadzone z wierzchołka ostrosłupa, są równe, to w podstawę ostrosłupa można wpisać okrąg, a środkiem tego okręgu jest spodek wysokości ostrosłupa.

Bogdan: Dobrze Basiu, ja też widzę tu 8 jednakowych ostrosłupów spełniających warunki zadania.

Eta: Bogdan .... podaj wynik, bo chcę wiedzieć, czy zgadza się z moimi obliczeniami PS: jest tu jeszcze jedno ciekawe zadanko, za chwilę podrzucę na naszą stronę

Eta: Basia< Bogdan! Zobaczcie zad> 3 ../forum/13785

Bogdan: Już jestem, zaraz podam rozwiązanie tego zadania.

Eta: Ja chcę tylko sprawdzić wynik

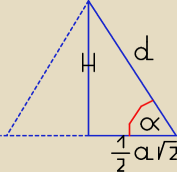
Bogdan: Wyznaczamy długość a oraz H mając dane d, α.

12a√2
	= cosα / *d√2
d

a = d√2cosα

H
	= sinα => H = dsinα
d

Objętość ostrosłupa jest równa ¹₆ objętości graniastosłupa V = ¹₆a²H = ¹₆ * 2d²cos²α * dsinα = ¹₃d³sinαcos²α Wynik taki, jaki podał gim

Eta: Dziękuję ....... gim......... to oczywiście ...... jaaaaaaaa

Bogdan: figlarka

Eta: Kobiety są przewrotne ( a szczególnie starsze ....

Bogdan: Nie strasz mnie

Eta: Czym Cię straszę? ... "młodością " ?

Bogdan: No tym, że kobiety są mniej przewrotne, gdy są młode. Spotykałem młode i przewrotne kobiety, a okazuje się, że mogą one być jeszcze bardziej niebezpieczne.