Na okręgu opisano trapez równoramienny Arekk: Na okręgu opisano trapez równoramienny ABCD. Ramiona BC i AD maja długość równą 4. Przekątne trapezu przecinają się w punkcie S i wiadomo, że |AS| = 3*|SC| Oblicz: a) długości podstaw trapezu b) pole tego trapezu Dzięki z góry za pomoc

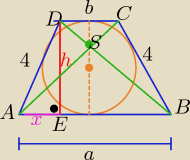
Eta: Z warunku wpisania okręgu w ten trapez mamy: a+b= 4+4 czyli a+b=8 oraz z tego,że |AS|=3|SC| wynika ,że

	a
ΔABS~ ΔCBS w skali k= 3 ⇒		=3 ⇒ a= 3b
	b

to: a+b=8 ⇒ 3b+b=8 ⇒ b=.......... to a=...........

	a−b
x=		=.......... h2= 42−x2 ⇒ h=.....
	2

	a+b
P=		*h=.........
	2

dokończ rachunki

Arekk: Wiszę Ci piwko

Eta:

rumpek: Wystarczy teraz tylko skorzystać, z tego, że △ASB ~ △DSC (k,k) Skala podobieństwa tych trójkątów wynosi k = 3, zatem podobieństwo pól to: P₁ = 9P₂ Oznaczmy sobie dłuższą podstawę: 3a, a krótszą a. Suma tych podstaw jest równa 4a. Z warunku, że na okręgu opisano trapez wiemy, że 2c = a + b ⇔ 4 + 4 = 3a + a ⇔ 8 = 4a ⇔ a = 2 Czyli |AB| = 6 oraz |CD| = 2, pozostało wyznaczyć h, nie jest to problem: 4² = h² + (2)² h² = 16 − 4 h² = 12 ⇔ h = 2√3

	(a + b)*h
P =
	2

	8 * 2√3
P(tr) =		= ...
	2

rumpek: jasny gwint

Eta: ..........

rumpek:

Eta: Od kiedy to popijają?

rumpek: od kiedy mają oceny wystawione

Eta: Jaka średnia? ( jeżeli można

rumpek: pewnie że można fajerwerków nie ma 4.3

rumpek: Zagadka: ciekawe co mi tak średnią obniżyło

Eta: Oooo ładnie ! a matma? 6 czy 5 ?

rumpek: 6 ona mi "wyciągnęła" najbardziej

Eta: Ojczysty język ! ma się rozumieć

Eta: No i superrr, tylko nie daj "plamy" na maturce

rumpek: zobaczmy jakie zadania będą Fajnie byłoby zastosować wzór P(tr) = (√P₁ + √P₂)² tak ojczysty język + wos, historia i inne takie

Eta: Można też taki P(tr) = (k+1)²*P₂ P₂ ( na twoim rys.)

rumpek: Takie już przyczajenie do tego wzorku <lubię to> Bardzo poręczny

Eta: No i jaki elegancki