 Witam!
Czy może mi ktoś bardzo łopatologicznie wytłumaczyć to zadanie:
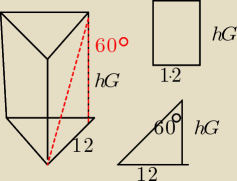
Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego tworzy z wysokością
graniastosłupa kąt o mierze 60stopni. Krawędź podstawy ma długość równą 12. Oblicz pole
powierzchni bocznej
tego graniastosłupa.
W internecie jest wiele rozwiązań ale żadnego nie rozumiem. Nie wiem jak wyliczyć brakujące
dane.
Ppb = 3 (a*b). Krawędź podstawy to jeden z boków prostokąta będącego ścianą tego graniastosłupa
a hG to drugi bok.
tg 60 = √3
Witam!
Czy może mi ktoś bardzo łopatologicznie wytłumaczyć to zadanie:
Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego tworzy z wysokością
graniastosłupa kąt o mierze 60stopni. Krawędź podstawy ma długość równą 12. Oblicz pole
powierzchni bocznej
tego graniastosłupa.
W internecie jest wiele rozwiązań ale żadnego nie rozumiem. Nie wiem jak wyliczyć brakujące
dane.
Ppb = 3 (a*b). Krawędź podstawy to jeden z boków prostokąta będącego ścianą tego graniastosłupa
a hG to drugi bok.
tg 60 = √3
| 12 | ||
√3 = | ||
| h |
| 12 | ||
h = | ||
| √3 |
| 144 | ||
Ppb = 3 * | ||
| √3 |
| 332 √3 | ||
Ppb = | ||
| 3 |
 .
.