rozwiąż nierówność czeski:

(x+5)(x+3)−(3x−1)(x−1)
	> 0
(x−1)(x+3)

może mi ktoś wytłumaczyć dlaczego tutaj mogę opuścić mianownik?

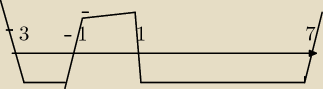
Jolanta: tak bym zrobiła x≠1 x≠−3 licznik x²+8x+15−3x²+4x−1=−2x²+12x+14 −2x²+12x+14=0 −x²+6x+7=0 Δ=36+28=64

	−6+8
x1=		=−1
	−2

	−6−8
x2=		=7
	−2

(x+1)(x−7)(x−1)(x+3)>0 x∊(−∞ ,−3) v(−1,1)v(7,∞)

lisek: prawie dobrze − brakuje minusa przed tą ostatnią nierównością, co zmienia wykres i rozwiązanie

Aga1.: Dwie ostatnie linijki są źle i oczywiście rysunek ( ale rysunek można zostawić)

−2(x+1)(x−7)
	>0
(x−1)(x+3)

−2(x+1)(x−7)(x−1)(x+3)>0//:(−2) (x+1)(x−7)(x−1)(x+3)<0 Odp. x∊(−3,−1)∪(1,7) Nie możesz opuścić mianownika, tylko możesz pomnożyć licznik razy mianownik. Inaczej mówiąć pomnożyć obie strony nierówności przez kwadrat mianownika.