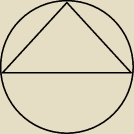
sprawdzi ktos stereometria xXxX: Promień podstawy stożka jest równy r, a kąt między tworzącą stożka i jego podstawą ma miarę α. Oblicz objętość kuli opisanej na tym stożku.

	r
Z moich obliczeń wynika że cos(2α−900)=
	R

	r
cos(−900+2α)=
	R

	r
sin2α=
	R

	r
R=
	sin2α

	4		r3
Vk=		π*		z tym cos nie jestem pewien.
	3		sin32α

xXxX: Godzio zerknij jak możesz

Godzio: Mogę

Godzio: Nieco prościej można Z twierdzenia sinusów:

2r		r
	= 2R ⇒ R =
sin(180 − 2α)		sin2α

	4
V =		πR3 = ...
	3

xXxX: Dzięki wielkie, jak zawsze najbardziej pomocny człowiek na tym forum i zawsze obecny W nagrode na kolacje

Godzio: Oj nie powiedziałbym, że najbardziej pomocny, kiedyś to jeszcze, ale teraz nie mam czasu

rumpek: Lub można jeszcze:

	r		r
cosα =		⇒ l =
	l		cosα

l
	= 2R
sinα

r   cosα
	= 2R
sinα

r		1
	*		= 2R
cosα		sinα

r
	= 2R / : 2
sinαcosα

	r		r
R =		=
	2sinαcosα		sin2α