s Klaudia: W trapezie równoramiennym podstawy mają 5cm i 11cm, natomiast przekątna trapezu jest jednocześnie dwusieczną kąta ostrego trapezu. Oblicz obwód i pole trapezu.

tim: Masz może odp?

Klaudia: nie mam

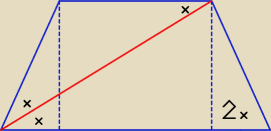
Bogdan: Podpowiedź. x − miara kąta

Eta: Pomagam Cierpliwości narysuję trapez

Eta: Witam Bogdanie Tym razem Ty nie dałeś informacji< że pomagasz? zatem mam już z "głowy"

xpt: Bogdan − skąd Ty wziąłeś informację, że trójkąt zawierający lewe ramię, przekątną i górną podstawę jest równoramienny ? Albo inaczej − skąd wziąłes ten "górny" x ?

xpt: A! Cofam pytanie − już widzę :P

Bogdan: Nie napisałem Eto pomagam, bo chciałem dać tylko podpowiedź i wycofuję się

Bogdan: Na tym xpt polegała podpowiedź, żeby ustalić, że w tym trapezie można zobaczyć trójkąt równoramieny, bo ta informacja jest kluczem do rozwiązania tego zadania.

Eta: Witam xpt Jeżeli przekątna trapezu równoramiennego zawiera się w dwusiecznej kąta to ramię trapezu = długości krótszej podstawy bo trójkąt ACD −− jest równoramienny bo kąty BAC = ACD −− jako naprzemianległe to i kąt DAC = ACD −−− z dwusiecznej!

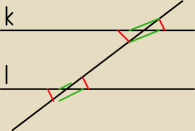
xpt: albo można tez tak − jeżeli dwie proste równoległe przetniemy prostą to odpowiednie kąty mają taką samą miarę (tak jak na rysunku ;) )

Klaudia: pole 32 i obwod 26?

Bogdan: Tak Klaudio