Planimetria Darth Mazut: Witam, dziś mam takie zadanko Trzeba wykazać, że odcinek łączący środki ramion dowolnego trapezu jest równoległy do podstaw a jego długość jest średnią arytmetyczną długości podstaw tego trapezu. Z góry dzięki pozdrawiam =) P.S. podpowiedzi też mile widziane

Darth Mazut: Odświeżam...

rumpek: Bry Wektory, wektory i jeszcze raz wektory (można podobieństwem ale żmudna robota )

Darth Mazut: No trudno, to jest planimetria, więc wektorów do tego używać raczej nie powinienem to po 1) a po 2) nawet jak to nie umiem ^

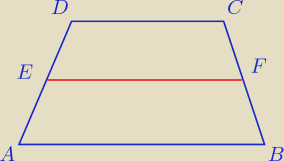
rumpek: Wektorowo:

	|AB| + |CD|
Teza: |EF| =		∧ AB || EF || CD
	2

⎧	|EF|→ = |AE|→ + |AB|→ + |BF|→
⎩	|EF|→ = |DE|→ + |CD|→ + |CF|→

(dodajemy wszystko co mamy w układzie) 1^o |DE|^→ oraz |AE|^→ się zerują (zwroty przeciwne) 2^o |CF|^→ oraz |BF|^→ się zerują (zwroty przeciwne) Ponadto: |EF| ||^→ (|AB|^→ + |CD|^→) (równoległe) Pozostaje nam: 2|EF| = |AB| + |CD| / : 2

	|AB| + |CD|
|EF| =
	2

c.n.u.

rumpek:

	a + b
|EF| =
	2

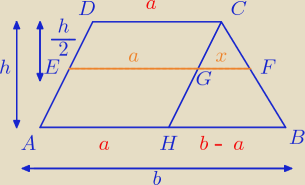
1^o Zauważmy, że odcinek |EG| ma taką miary co górna podstawa trapezu (cała ta figura to romb), zatem |EG| jest równoległy. 2^o Z podobieństwa trójkątów: △CFG ~ △HBC

h   2		x
	=
h		b − a

h		1		x
	*		=
2		h		b − a

1		x
	=		[a,b > 0]
2		b − a

2x = (b − a) / : 2

	b − a
x =
	2

3^o Teraz pozostało zsumować to co nam zostało na odcinku |EF| = a + x

	b − a		2a + b − a		a + b
|EF| = a +		=		=
	2		2		2

c.n.u.

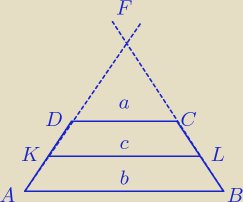
rumpek: Kolejny sposób to: teraz samym podobieństwem zupełnie podstawiamy odpowiednie dane, zauważ, że są trzy trójkąty: △ABF ~△KLF ~ △DCF (k,k,k) itp.

b.: @19:35: 1. dlaczego kąty FKL oraz FDC mają taką samą miarę? nie wiemy, że KL jest równoległe do podstaw, to należy udowodnić 2. osobnego rozważenia wymaga przypadek równoległoboku (a w zasadzie jeszcze symetrycznej sytuacji, w której dłuższą podstawą jest CD).

rumpek: 1. nauczycielka, który mnie uczy powiedziała bodajże 2 lata temu, że egzaminatorom wystarczy zauważenie, że te trójkąty są podobne, bez dodatkowych dowodów; dowód sam jako główny, bez pobocznych a udowodnić to co pisze b. nie jest problemem 2. owszem, chyba że w zadaniu mamy podane, że b > a, gdzie |AB| = b i |CD| = a

Darth Mazut: Hmm, wykorzystałem to, że prosta łącząca środki ramion dzieli wysokość trapezu na 2 równe części, i po podstawieniu do wzorów na pola faktycznie wychodzi, że ten odcinek łączący jest dwa razy mniejszy od sumy podstaw, natomiast mam jeszcze problem z załapaniem warunku równoległości...

b.: 1. jak dla mnie samo zauważenie że te trójkąty są podobne (kkk) jest równoważne zauważeniu, że CD i KL są równoległe −− czyli dowodu brakuje. Żeby zobaczyć, że tak jest, można się zastanowić, w którym miejscu w 'dowodzie podobieństwa' wykorzystałeś, że |DK|=|KA| oraz |CL|=|BL|?

rumpek: b. przecież nie udowadniałem trzecim sposobem , a że są równoległe tw. Talesa

Darth Mazut: Ok, to powiem nauczycielce, że tak jest i koniec

rumpek: Darth Mazut najlepiej weź sposób 1 bo jest piękny w swej prostocie lub 2 bo też jest pikny

Darth Mazut: no ale sposób 2 nie wykazuje chyba bezposrednio że prosta jest równoległa do podstaw?

rumpek: Tak jak pisałem, zastosuj tw. Talesa. to powinieneś znać z 1 klasy

Darth Mazut: taaa, znam ale jak to niby zastosować? w sensie że co do czego mam przyrównać?

rumpek: podobnie jak tu: https://matematykaszkolna.pl/strona/3005.html

b.: zgadza się, albo podobnie jak tu: 533 (z tym że tam jest tw. Talesa a nie odwrotne, ale rysunek jest bliższy naszej sytuacji).