kolos z matematyki blogther: Zadanie 1 Wyznacz ekstrema lokalne funkcji f(x,y) = x² + 2x + y² − 4xy + 7 Zadanie 2 Oblicz pole obszaru ograniczonego przez krzywe y = x, y² = x Zadanie 3 Oblicz objetosc bryły ograniczonej przez 1 ≤ x² + y² ≤4, z ≥ 0, z ≤ x² + y² Zadanie 4 Policz mase bryły ograniczonej przez płaszczyzny z = y², z = 0, x = 0, z = x brakuje danych bo pani zapomniała napisac ale jak by ktos mogł wyznaczyc ta bryłe czy co to bedzie i dla jakis przykładowych danych policzyc zeby był jakis schemat rozwiazywania takich zadan.

mala: http://www.wolframalpha.com/input/?i=y+%3D+x%2C+y^2+%3D+x+

blogther: moze ktos sie wypowiedziec

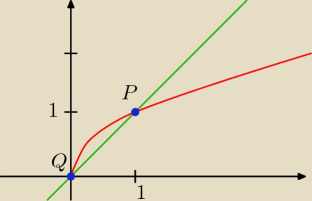
blogther: Zadanie 2 zielina prosta y = x czerwona krzywa y² = x ⇒ y = √x na niebiesko zaznaczyłem punkty wspolne czyli punkty przeciecia sie krzywych wyznaczyłem je w nastepujacy sposob rozwiazuja taki oto układ rownan

⎧	y=x
⎩	y=√x

x = √x |⁽⁾² x² = x x² − x = 0 x(x − 1) = 0 x = 0 lub x = 1 i wspołrzedne punktów P(1,1) a Q(0,0) pole policze ze wzoru P = ∫(f(x) − g(x))dx gdzie f(x) to funkcja ograniczajaca szukane pole obszaru od gory czyli f(x) = √x a g(x) ogranicza od dołu czyli g(x) = x zakres a= 0 b = 1 P = ∫( √x − x)dx = ∫√xdx − ∫xdx = ∫x^1₂dx − ∫xdx = ²₃x^3₂| − ¹₂x²| no i teraz oczywiscie nie zapominamy ze mamy obszar a=0 i b= 1 ktory powinnismy zapisac nad całka to znaczy a pod całka a b nad całka tak samo na kreskach | czyli mam y cos takiego P = ∫( √x − x)dx = ∫√xdx − ∫xdx = ∫x^1₂dx − ∫xdx = ²₃x^3₂| − ¹₂x²| = ²₃(1^3₂ − 0^3₂) − ¹₂(1² − 0²) = ²₃ − ¹₂ = = ⁴₆ − ³₆= ¹₆ [ j² ] czy moze ktos to sprawdzic czy wszystko jest poprawnie

blogther: pomoze ktos?