planimetria
KK: Kąty ostre między przekątną równoległoboku a jego bokami mają miary α i β, oblicz obwód i pole
tego równoległoboku
12 kwi 13:07
KK: proszę
12 kwi 13:19
KK: a jeszcze jest dana przekatna − d
12 kwi 13:22
MQ: Najpierw prześlę rysunek, potem rozwiązanie:
12 kwi 14:04
MQ:
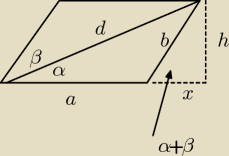
12 kwi 14:08
MQ: Wychodzi:
h=dsinα
| | cos(α+β) | |
a=d(cosα−sinα |
|
|
| | sin(α+β) | |
| | sinα*sinβ | |
Biorąc Pole=a*h dostajemy Pole=d2 |
|
|
| | sin(α+β) | |
| | sinα+sinβ | |
Obwód=2a+2b dostajemy Obwód=2d |
|
|
| | sin(α+β) | |
12 kwi 14:15
MQ: Jeśli się gdzieś oczywiście w przeliczeniach sinusów i cosinusów nie rąbnąłem, bo było to
żmudne.
12 kwi 14:17
