Punkty wspólne prostej z okręgiem Aneta: Ile punktów wspólnych ma prosta o równaniu y= −x+2 z okręgiem o środku w początku układu współrzędnych i promieniu 2 ?

kam: S=(0,0) r= 4 Rozwiąż równanie x² + y² = 4 y= −x +2

emagnuski: Wzór ogólny na okrąg to: (x − x₀)² + (y − y₀)² = r² S(0,0) Po podstawieniu dostajemy x² + y² = 4 trzeba wyliczyć z tego wzoru y, przyrównać do Twojego wzoru liniowej i obliczyć

MQ: Po co tak skomplikowanie? Wystarczy to narysować, albo zauważyć, że prosta przechodzi przez punkty (0,2) i (2,0), które należą do okręgu, bo promień 2 i środek w początku układu wsp. Więcej nie może mieć, bo prosta może przecinać okrąg w co najwyżej 2 pkt.

emagnuski: y = √4−x² y = −x+2 √4−x² = −x + 2 /()² 4−x² = (2−x)² 4−x² = 4−4x+x² 2x²−4x=0 x²−2x = 0 x(x−2) = 0 x = 0 lub x = 2 Dla x = 0: y = −0 + 2 = 2 P(0,2) Dla x = 2: y = −2 + 2 = 0 P(2,0)

Aneta: dzięki wielkie

LedZ: MQ twoja metoda jest dobra, ale dla podstawy na rozszerzeniu nie można odczytywać z rysunków, trzeba wszystko poprzeć obliczeniami

MQ: @LedZ Przeczytaj mój post po wyrazie "albo".

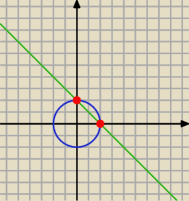
emagnuski: Tak, może i łatwiej, ale na kartce. Rysowałem to z 5 minut. Czerwone punkty to ów punkty przecięcia.