ZALICZENIE Z MATMY
K2K7: POTRZEBUJĘ POMOCY Z 10ZADANIAMI JAK TO OBLEJE TO MAM SIERPIEŃ A JESTEM W 3KLASIE LO WIĘC BĘDZIE
TO OZNACZAĆ KONIEC Z MATURĄ ITD.
BŁAGAM POMÓŻCIE MI
11 kwi 19:22
emagnuski: To dawaj te zadania
11 kwi 19:22
Cancer0s: Dawaj dawaj

11 kwi 19:25
K2K7: 1.Pole trójkąta równobocznego jest równe 4
√3. Jaka długość ma jego wysokość

?
2.Wysokość trójkąta równobocznego ma długość 6 jaką długość ma bok tego trójkąta
3.Ramiona trójkąta równoramiennego mają długość 10cm.Oblicz pole i obwód tego trójkąta wiedząc
że kąt między ramionami ma miarę 120 stopni
4.W trapezie prostokątnym Kąt ostry ma miarę 45 stopni a dłuższe ramie i krótsza przekątna
12cm.Oblicz obwód i pole trapezu
5.Znajdź x i y wiedząc że (2,x,y) to ciąg arytmetyczny a (3,x+2,y+6) to ciąg geometryczny
6.Trzy liczby których suma wynosi 16 tworzą rosnący ciąg arytmetyczny. Jeśli do tych liczb
dodamy kolejno 1,1 i 3 to otrzymamy, trzy kolejne wyrazy ciągu geometrycznego również
rosnącego.Znajdź te liczby.
7.Wyrazami ciągu arytmetycznego są liczby dwucyfrowe,które przy dzieleniu przez 5 dają resztę
2.Wyznacz sumę tych liczb.
8.Rozwiąż równanie wiedząc że jego lewa strona jest sumą ciągu arytmetycznego
a.8+6+4+...x=−220
b.(x+1)+(x+2)+...(x+28)=155
To wszystko było 8 wiem że niektóre są do siebie podobne ale nie myślcie że chce wszystko
zwalić na was po prostu oprócz tych mam jeszcze 6 zadań które sam robię bo w miarę je ogarniam
a bardzo szybko muszę je mieć zrobione bym zdążył się nauczyć na piątek na spr z tego.Tylko wy
mi możecie pomóc będę bardzo wdzięczny i jak będę potrafił to się odwdzięczę
11 kwi 19:35
kylo1303: Jesli nie chca cie dopuscic to moze cos w tym jest

Poza tym skad pewnosc ze zdasz mature
W trojakcie rownobocznym o boku "a", wysokosci "h" i Polu "P" masz takie zaleznosci:
11 kwi 19:37
emagnuski: 8.Rozwiąż równanie wiedząc że jego lewa strona jest sumą ciągu arytmetycznego
a.8+6+4+...x=−220
a
1 = 8
r = a
2 − a
1 = 6−8 = −2
S
n = −220
a
n = x
a
n = a
1 + (n−1)r
a
n = 8 + (n−1)(−2)
a
n = 8 −2n + 2
a
n = 10 − 2n
−440 = (18 − 2n)n
−440 = 18n − 2n
2
2n
2 − 18n − 440 = 0
n
2 − 9n − 220 = 0
Δ = 81 + 880 = 961 =
√312
| | 9−31 | |
n1 = |
| = −11 − sprzeczne, numer wyrazu nie może mieć wartości ujemnej |
| | 2 | |
a
n = a
20 = a
1 + (n−1)r
a
20 = 8 + (19)(−2) = 8 − 38 = −30
x = −30
11 kwi 19:51
emagnuski: b.(x+1)+(x+2)+...(x+28)=155
Z kolejnych liczb w nawiasach (1,2,...,28) zauważam że ilość dodanych liczb jest równa 28 (n =
28)
(x+1)+(x+2)+...(x+28) = 28x + (1+2+...+28)
Rozważam nawias (1+2+...+28):
a
1 = 1
n = 28
r = 1
a
n = a
28 = 28
| | 1 + 28 | |
Sn = |
| 28 = 29*14 = 406 |
| | 2 | |
Podstawiam wyliczoną sumę:
28x + (406) = 155
28x = 155 − 406
28x = −251
11 kwi 19:59
emagnuski: Nieładny wynik, ale raczej dobry. Poddam weryfikacji kolegi kujona geniusza.
11 kwi 20:00
psik: 5. z własności ciągu arytm : 2x=2+y oraz z własności ciągu geometrycznego : (x+2)2=3(y+6)
liczę z drugiej własności x2 + 4x + 4 = 3y + 18 . Z pierwszej własności podstawiam y = 2x−2
x2 + 4x +4 −3(2x−2) −18 = 0 => x2 + 4x + 4 − 6x −12 = 0 => x2 −2x − 8 = 0 rozwiązać równanie
kwadratowe i masz z tego x ( dwie wartości), potem y (też dwie wartości)
11 kwi 20:10
emagnuski: 7.Wyrazami ciągu arytmetycznego są liczby dwucyfrowe,które przy dzieleniu przez 5 dają resztę
2.Wyznacz sumę tych liczb.
Są to liczby:
11, 12, 13, 14, 16, 17, 18, 19, 21, ..., 96, 97, 98, 99
Można obliczyć to obliczając sumę wszystkich liczb dwucyfrowych i odejmując od niej sumę liczb
dwucyfrowych podzielnych bez reszty przez 5, czyli:
10, 15, 20, 25, ..., 90, 95
Wzór ogólny na sumę wyrazów ciągu o różnicy r:
Obliczam sumę liczb dwucyfrowych:
n = 90 (aby je obliczyć najłatwiej jest odjąć 9 od 99)
a
1 = 10
a
90 = 99
r = 1
| | 2*10 + (90−1)1 | |
S90 = |
| 90 = (20+89)45 = 109*45 = 4905 |
| | 2 | |
Obliczam sumę liczb podzielnych przez 5:
n = 19 (można policzyć nawet na palcach)
a
1 = 10
a
19 = 95
r = 5
| | 2*10 + (19−1)5 | | 19 | | 19 | |
S19 = |
| 19 = (20+18)* |
| = 38* |
| = 361 |
| | 2 | | 2 | | 2 | |
S
szukana = S
90 − S
19 = 4905 − 361 = 4544
11 kwi 20:13
emagnuski:
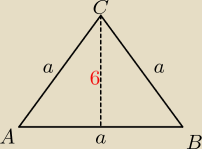
2.Wysokość trójkąta równobocznego ma długość 6 jaką długość ma bok tego trójkąta
Prawie to samo z zad. 1
| | 6*2√3 | |
a = |
| = 2*2√3 = 4√3 |
| | 3 | |
Wszystkie boki rzecz jasna takie same, równe 4
√3
11 kwi 20:20
psik: dając resztę 2 to nie wszystkie liczby niepodzielne przez 5. To : 12,17,22,27,32,37,...,97,
ciąg arytmetyczny o r = 5 , a1 = 12 i an = 97. Liczbę wyrazów n liczymy ze wzoru na an :
97 = 12+(n−1)*5
85 = 5n − 5
90 = 5n
n = 18
I na wzór na sumę.
11 kwi 20:29
emagnuski:
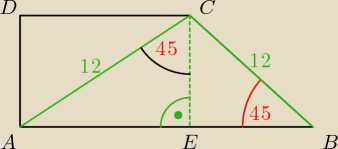
4.W trapezie prostokątnym Kąt ostry ma miarę 45 stopni a dłuższe ramie i krótsza przekątna
12cm.Oblicz obwód i pole trapezu
ΔEBC jest równoboczny, więc |EB| = |EC|
Z ΔEBC i tw. Pit.:
|BC|
2 = |EB|
2 + |EC|
2
12
2 = |EB|
2 + |EB
2|
144 = 2|EB|
2
77 = |EB|
2
|EB| =
√77
|EB| = |EC| = |AD| = h =
√77
Może nie bardzo widać to z rysunku, ale:
|AE| = |CD| = |EC| =
√77
|AB| = |AE| + |BE| = 2
√77
Obw =
√77 +
√77 + 2
√77 + 12 = 4
√77 + 12 = 4(3 +
√77)
| | (a+b)h | | (2√77 + √77)√77 | | 3√77√77 | | 3*77 | | 1 | |
P = |
| = |
| = |
| = |
| = 115 |
| |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
Też komuś pokażę, mimo że tu już jest ładny wynik.
11 kwi 20:34
psik: 144/2 = 72 wtedy EB = √72 = 6√2
11 kwi 20:45
emagnuski: O właśnie, więc √77 trzeba zamienić na 6√2 i przeliczyć.
11 kwi 20:47
emagnuski:
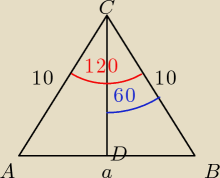
3.Ramiona trójkąta równoramiennego mają długość 10cm.Oblicz pole i obwód tego trójkąta wiedząc
że kąt między ramionami ma miarę 120 stopni
Z ΔBCD:
|CD| = |BC|cos60
h = 5
|DB| = |BC|sin60
a = 2|DB| = 10
√3
Obw = 10
√3 + 2*10 = 10(2+
√3)
11 kwi 20:49
emagnuski: A co do
7.Wyrazami ciągu arytmetycznego są liczby dwucyfrowe,które przy dzieleniu przez 5 dają resztę
2.Wyznacz sumę tych liczb.
To nie zauważyło mi się tego że mają dawać resztę 2, policzyłem tak gdyby reszta była dowolna,
ale Piotrek "poprawił".
11 kwi 20:51
Eta:
@
emagnuski
Startuj zamiast
K2K7 do matury

11 kwi 21:00
psik: emagnuski też piszę maturę

. I wkręcił się w pomaganie tutaj ludziom

.
11 kwi 21:05
Eta:
Jak widać ............ właściciela tego postu nawet nie ma na forum

11 kwi 21:06
psik: 
11 kwi 21:10
emagnuski: Robię to nie tylko dla innych, ale też dla siebie, matura się sama nie napisze.
11 kwi 21:11
K2K7: Słyszałem wiele o tej stronie i nie raz z niej korzystałem (w szczególności od miesiąca kiedy
pojąłem w kilka tygodni materiał którego przez 2 lata nie mogłem ogarnąć−ale jak mnie przybili
do muru to trzeba)ale nie miałem pojęcia że tyle osób będzie chciało mi pomóc w szczególności
emagnuski ale inni również bardzo mi pomogli (i mam nadzieję że nadal pomogą) nie wiem
jak ja się wam za to odwdzięczę ale chyba nie w matmie

ale jak będziecie mieli jakieś
pomysły to śmiało (chociaż dobry to ja jestem tylko z historii,wos−u,polaka(tak w miarę) i
ogólnie humanistyczne przedmioty ale za to mam bzika na punkcie motoryzacji więc jakby ktoś
chciał kupić jakieś autko czy coś mogę udzielić jakiś info wiem że raczej nikt się nie zgłosi
ale chciałbym się jakoś odwdzięczyć bo wiele dla mnie zrobiliście )
A odpowiadając na pytanie kylo1303
Jesli nie chca cie dopuscic to moze cos w tym jest Poza tym skad pewnosc ze zdasz maturę
Co do matury fakt nie mam pewności czy ją zdam (gdyby nie ta matma to pewny bym był na 90%)
ale jeżeli będę się starał bo uważam że teraz robię postępy późno ale zawsze to mi to już
wystarczy ponieważ będę miał tą satysfakcję że próbowałem i podszedłem wynik już mnie tak nie
interesuję bo ta matura nie jest mi do niczego potrzebna...a to dlaczego to już zostawię dla
siebie.
11 kwi 22:07
K2K7: emagunski− zauważyłem że wdarł ci się błąd w zadaniu nr.7 liczb 2−cyfrowych podzielnych przez 5
jest
18 nie 19 ale wiadomo każdemu się zdarza

11 kwi 22:59
K2K7: Cofam to nie dojechałem wtedy do końca postów sorry
11 kwi 23:09

 ?
2.Wysokość trójkąta równobocznego ma długość 6 jaką długość ma bok tego trójkąta
3.Ramiona trójkąta równoramiennego mają długość 10cm.Oblicz pole i obwód tego trójkąta wiedząc
że kąt między ramionami ma miarę 120 stopni
4.W trapezie prostokątnym Kąt ostry ma miarę 45 stopni a dłuższe ramie i krótsza przekątna
12cm.Oblicz obwód i pole trapezu
5.Znajdź x i y wiedząc że (2,x,y) to ciąg arytmetyczny a (3,x+2,y+6) to ciąg geometryczny
6.Trzy liczby których suma wynosi 16 tworzą rosnący ciąg arytmetyczny. Jeśli do tych liczb
dodamy kolejno 1,1 i 3 to otrzymamy, trzy kolejne wyrazy ciągu geometrycznego również
rosnącego.Znajdź te liczby.
7.Wyrazami ciągu arytmetycznego są liczby dwucyfrowe,które przy dzieleniu przez 5 dają resztę
2.Wyznacz sumę tych liczb.
8.Rozwiąż równanie wiedząc że jego lewa strona jest sumą ciągu arytmetycznego
a.8+6+4+...x=−220
b.(x+1)+(x+2)+...(x+28)=155
To wszystko było 8 wiem że niektóre są do siebie podobne ale nie myślcie że chce wszystko
zwalić na was po prostu oprócz tych mam jeszcze 6 zadań które sam robię bo w miarę je ogarniam
a bardzo szybko muszę je mieć zrobione bym zdążył się nauczyć na piątek na spr z tego.Tylko wy
mi możecie pomóc będę bardzo wdzięczny i jak będę potrafił to się odwdzięczę
?
2.Wysokość trójkąta równobocznego ma długość 6 jaką długość ma bok tego trójkąta
3.Ramiona trójkąta równoramiennego mają długość 10cm.Oblicz pole i obwód tego trójkąta wiedząc
że kąt między ramionami ma miarę 120 stopni
4.W trapezie prostokątnym Kąt ostry ma miarę 45 stopni a dłuższe ramie i krótsza przekątna
12cm.Oblicz obwód i pole trapezu
5.Znajdź x i y wiedząc że (2,x,y) to ciąg arytmetyczny a (3,x+2,y+6) to ciąg geometryczny
6.Trzy liczby których suma wynosi 16 tworzą rosnący ciąg arytmetyczny. Jeśli do tych liczb
dodamy kolejno 1,1 i 3 to otrzymamy, trzy kolejne wyrazy ciągu geometrycznego również
rosnącego.Znajdź te liczby.
7.Wyrazami ciągu arytmetycznego są liczby dwucyfrowe,które przy dzieleniu przez 5 dają resztę
2.Wyznacz sumę tych liczb.
8.Rozwiąż równanie wiedząc że jego lewa strona jest sumą ciągu arytmetycznego
a.8+6+4+...x=−220
b.(x+1)+(x+2)+...(x+28)=155
To wszystko było 8 wiem że niektóre są do siebie podobne ale nie myślcie że chce wszystko
zwalić na was po prostu oprócz tych mam jeszcze 6 zadań które sam robię bo w miarę je ogarniam
a bardzo szybko muszę je mieć zrobione bym zdążył się nauczyć na piątek na spr z tego.Tylko wy
mi możecie pomóc będę bardzo wdzięczny i jak będę potrafił to się odwdzięczę
 Poza tym skad pewnosc ze zdasz mature
W trojakcie rownobocznym o boku "a", wysokosci "h" i Polu "P" masz takie zaleznosci:
Poza tym skad pewnosc ze zdasz mature
W trojakcie rownobocznym o boku "a", wysokosci "h" i Polu "P" masz takie zaleznosci:
 2.Wysokość trójkąta równobocznego ma długość 6 jaką długość ma bok tego trójkąta
Prawie to samo z zad. 1
2.Wysokość trójkąta równobocznego ma długość 6 jaką długość ma bok tego trójkąta
Prawie to samo z zad. 1
 4.W trapezie prostokątnym Kąt ostry ma miarę 45 stopni a dłuższe ramie i krótsza przekątna
12cm.Oblicz obwód i pole trapezu
ΔEBC jest równoboczny, więc |EB| = |EC|
Z ΔEBC i tw. Pit.:
|BC|2 = |EB|2 + |EC|2
122 = |EB|2 + |EB2|
144 = 2|EB|2
77 = |EB|2
|EB| = √77
|EB| = |EC| = |AD| = h = √77
Może nie bardzo widać to z rysunku, ale:
|AE| = |CD| = |EC| = √77
|AB| = |AE| + |BE| = 2√77
Obw = √77 + √77 + 2√77 + 12 = 4√77 + 12 = 4(3 + √77)
4.W trapezie prostokątnym Kąt ostry ma miarę 45 stopni a dłuższe ramie i krótsza przekątna
12cm.Oblicz obwód i pole trapezu
ΔEBC jest równoboczny, więc |EB| = |EC|
Z ΔEBC i tw. Pit.:
|BC|2 = |EB|2 + |EC|2
122 = |EB|2 + |EB2|
144 = 2|EB|2
77 = |EB|2
|EB| = √77
|EB| = |EC| = |AD| = h = √77
Może nie bardzo widać to z rysunku, ale:
|AE| = |CD| = |EC| = √77
|AB| = |AE| + |BE| = 2√77
Obw = √77 + √77 + 2√77 + 12 = 4√77 + 12 = 4(3 + √77)
 3.Ramiona trójkąta równoramiennego mają długość 10cm.Oblicz pole i obwód tego trójkąta wiedząc
że kąt między ramionami ma miarę 120 stopni
Z ΔBCD:
3.Ramiona trójkąta równoramiennego mają długość 10cm.Oblicz pole i obwód tego trójkąta wiedząc
że kąt między ramionami ma miarę 120 stopni
Z ΔBCD:

 . I wkręcił się w pomaganie tutaj ludziom
. I wkręcił się w pomaganie tutaj ludziom  .
.


 ale jak będziecie mieli jakieś
pomysły to śmiało (chociaż dobry to ja jestem tylko z historii,wos−u,polaka(tak w miarę) i
ogólnie humanistyczne przedmioty ale za to mam bzika na punkcie motoryzacji więc jakby ktoś
chciał kupić jakieś autko czy coś mogę udzielić jakiś info wiem że raczej nikt się nie zgłosi
ale chciałbym się jakoś odwdzięczyć bo wiele dla mnie zrobiliście )
A odpowiadając na pytanie kylo1303
Jesli nie chca cie dopuscic to moze cos w tym jest Poza tym skad pewnosc ze zdasz maturę
Co do matury fakt nie mam pewności czy ją zdam (gdyby nie ta matma to pewny bym był na 90%)
ale jeżeli będę się starał bo uważam że teraz robię postępy późno ale zawsze to mi to już
wystarczy ponieważ będę miał tą satysfakcję że próbowałem i podszedłem wynik już mnie tak nie
interesuję bo ta matura nie jest mi do niczego potrzebna...a to dlaczego to już zostawię dla
siebie.
ale jak będziecie mieli jakieś
pomysły to śmiało (chociaż dobry to ja jestem tylko z historii,wos−u,polaka(tak w miarę) i
ogólnie humanistyczne przedmioty ale za to mam bzika na punkcie motoryzacji więc jakby ktoś
chciał kupić jakieś autko czy coś mogę udzielić jakiś info wiem że raczej nikt się nie zgłosi
ale chciałbym się jakoś odwdzięczyć bo wiele dla mnie zrobiliście )
A odpowiadając na pytanie kylo1303
Jesli nie chca cie dopuscic to moze cos w tym jest Poza tym skad pewnosc ze zdasz maturę
Co do matury fakt nie mam pewności czy ją zdam (gdyby nie ta matma to pewny bym był na 90%)
ale jeżeli będę się starał bo uważam że teraz robię postępy późno ale zawsze to mi to już
wystarczy ponieważ będę miał tą satysfakcję że próbowałem i podszedłem wynik już mnie tak nie
interesuję bo ta matura nie jest mi do niczego potrzebna...a to dlaczego to już zostawię dla
siebie.
