dowód zbk : Wykaż, że jeśli A, B są dowolnymi zdarzeniami przestrzeni Ω, to P(A uB) = P(A) + P(B) – P(A∩ B).

zbk : prosze o pomoc jak ma ktos pomysl

zbk : ?//////////////////////////////////////

Krzysiek: A∪B=A∪(B\A) P(A∪B)=P(A)+P(B\A)+P(A∩B)−P(A∩B) (P(B\A)+P(A∩B) =P(B)) czyli: P(A∪B)=P(A)+P(B)−P(A∩B)

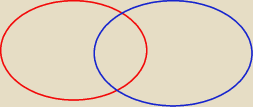
LedZ: czerwony to zbiór zdarzeń A niebieski B najpierw wykonujemy działania na zbiorach A=(A\B)∪(A∩B) (A\B)∩(A∩B)=∅ P(A)=P(A\B)+P(A∩B) A∪B=(A\B)∪B (A\B)∩B=∅ P(A∪B)=P(A\B)+P(B) P(A∪B)=P(A)+P(B)−P(A∩B)

zbk : dzięki wielkie