?? Lidka: Podaj dziedzine i zbiór wartości funkcji,sporządź wykres. k)F(x)=|x| l)f(x)=3−|x| nie radzę sobie ztymi wartościami.Prosze o wytlumaczenie,o takie wytłumaczenie by pojąć to mógł umysł humanistyczny Dzięki!

Lidka: wartościami bezwględnymi* bo tam będzie jakeis lub bądź i ...

MQ: Dawniej "umysł humanistyczny" znaczyło to samo co "umysł wszechstronny", więc nie nadużywaj pojęcia. A co do |x|, to oznacza nic tylko tyle, że bierzesz liczbę bez znaku, więc dla: k) f(x)=|x| oznacza, że wartości będą dodatnie, czyli f(x)≥0 dla każdego x albo inaczej pisząc f(x)∊<0;∞) l) f(x)=3−|x| oznacza, że od 3 odejmujesz liczbę dodatnią, bo |x|≥0, czyli wartości funkcji będą od 3 w dół, czyli f(x)≤3 albo f(x)∊(−∞;3>

Lidka: Dziekuje.pisząc,że jestem umysłem humanistycznym chciałam tylko zwrócic uwage na to,że prosze o jakies proste wytłumaczenie,a nie wytłumaczenie w tzw.języku matematycznym.

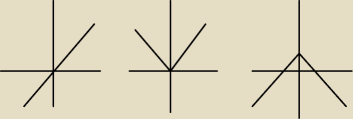
LedZ: pierwszy wykres to wykres funkcji f(x)=x przykład k) można zrobić na dwa sposoby 1) wziąć wartość bezwzględną z y, czyli całości funkcji dla np. funkcji y=3x+5 po przekształceniu |y| wygląda ona tak: y=|3x+5|, "zamykamy" w wartość bezwzględną całą funkcję dla wykresu wygląda to tak, że to, co jest pod osią OX "przerzucamy" nad oś, odbijamy to w symetrii, ale część będącą nad osią zostawiamy bez zmian 2) wziąc wartość bezwzględną tylko z x np. dla funkcji y=x+16 po przekształceniu |x| wygląda ona tak: y=|x|+16, "zamykamy" w wartość bezwzględną tylko x! la wykresu wygląda to tak, że to, co jest po lewej stronie osi OY przestaje dla nas istnieć, nie przejmujemy się tym, natomiast to co jest po prawej odbijamy na drugą stronę, powstaje obraz jak przy przyłożeniu lusterka dla funkcji f(x)=|x| te przekształcenia są równoznaczne, przybliżony obraz wykresu pokazuje drugi rysunek przykład l) proponuję zacząć od funkcji f(x)=x, następnie przekształcić za pomocą |x| lub |y| (w przykładzie k widać, że są one sobie równoznaczne), następnie by otrzymać znak minus przed |x| przekształcamy wykres w symetrii wzgl osi OX (gdybyśmy przekształcili wzgl osi OY otrzymalibyśmy |−x|) a poźniej przesuwamy o wektor [0,3]

Lidka: w przykładzie k zrobiłam tak,że za x podtawiłam liczby od −3 do 3 ,wyliczyłam,wyszło mi y=3,2,1,0,1,2,3la wykresu wygląda to tak, że to, co jest po lewej stronie osi OY przestaje dla nas istnieć, nie przejmujemy się tym, natomiast to co jest po prawej odbijamy na drugą stronę, powstaje obraz jak przy przyłożeniu lusterka − ni9e do końca rozumiem,ale ostatecznie wyszedł mi taki wykres jak powyżej.dzieki!

Lidka: oj tak teraz patrze i nie wyszło mi l... mam tylko połowę po prawej stronie.kurde,nie rozumiem

LedZ: narysuj to, co ci wyszło

Lidka: czyli robiąc to drugim sposobem moge po prostu 'przerysowac'prawą strone na lewą? tak jakos dziwnie

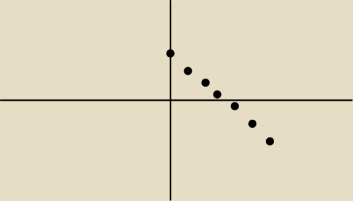
Lidka: cos podobnego...

LedZ: dokładnie, taki jest sposób na |x| bo skoro np. |x|=3 to x może być 3 i −3 i ta −3 jest odbiciem 3 względem osi OY czyli taka wartość, jaka była dla 3, musi być dla −3 czyli jaka wartość była dla prawej strony wykresu (tam gdzie x>0) to musi być taka sama dla lewej (x<0), jest jej odbiciem robiąc kilka takich wykresów i nabierając wprawy, nie bedziesz musiała liczyć poszczególnych x−ów, tylko po prostu to przerysujesz

Lidka: czyli mój bład polegał na tym,że nie wzięłam liczb ujemnych (do dziedziny funkcji,tak?

Lidka: nie....

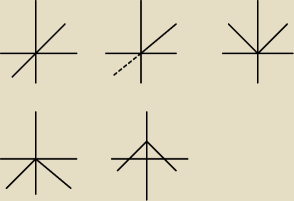
LedZ: pamiętaj, żeby wykresy rysować jako linie, a nie punkty tak, liczby ujemne też musisz uwzględnić pokażę ci krok po kroku jak to zrobić bez podstawiania konkretnych liczb pierwszy wykres to funkcja f(x)=x teraz chcemy narysować wykres f(x)=|x| w drugim zaznaczyłam przerywaną linią, o której części wykresu możemy "zapomnieć". ta część, która zostaje, odbijamy ją na drugą stronę i mamy wykres funkcji f(x)=|x| dla drugiego podpunktu trzeba jeszcze zrobić dwie operacje najpierw stawiamy znak minus przed wartością bezwzględną (chcemy otrzymać f(x)= −|x|). to nic innego, jak stawianie znaku minus przed "całą" funkcją, a żeby tak zrobić, to odbijamy wykres w symetrii OX (gdy mówimy o symetrii nie "zapominamy o żadnej części wykresu, jak w przypadku |x|) i teraz, by otrzymać f(x)=−|x|+3 musimy przesunąć wykres o wektor [0,3] (3 jednostki w górę) 0 dlatego, że nic się nie zmienia "bezpośrednio obok" iksa (jeżeli byłoby np [1,3} to wyszłoby nam −|x−1|+3, tak przy okazji wektorów) piąty wykres to wykres ostateczny

Lidka: Czyli ogólnie rzecz biorąc wszędzie powinnam nie zapominac o liczbach uejmnych,z wyjatkiem √x ... Bardzo mi pomogleś,pomoglaś !dzięki za poświęcony czas

LedZ: tak, nie zapominiaj o nich i jeśli nie jesteś na rozszerzeniu, to raczej nie poznasz funkcji logarytmicznej, dla której zawsze x>0