pomoc Jaa. : Kochani, szukam osób które byłyby chętne pomóc mi zrobić 20 zadań na zaliczenie matematyki. Nigdy w życiu nie poradzę sobie sama a wiem że tutaj zawsze można na kogoś liczyć... Proszę..

Alkain: Dawaj po kolei coś na pewno się zrobi

Jaa. : chętnych zapraszam na gg 4183173. Za jaką kolwiek pomoc będę bardzo wdzięczna...

Mateusz: na gg ciężko sie pomaga tu jest prosciej poza tym komu bedzie sie chciało wykonac te czynnosci: zaznacz numer gg−−> nacisnij ctrl+C−−−> przenies sie na gg −−−−−> kliknij kontakty−−−−>kliknij dodaj−−−−> nacisnij ctrl+V−−−−−−> kliknij dodaj osobe−−−−−−> kliknij dwa razy na kontakt−−−−−−−−>napisz wiadomosc powitalną

Święty: Komu by się chciało pisać taką instrukcję w poście

Sylwia: pisałam z tel więc cięzko było sory na głupka wyszłam już piszę zadania

Sylwia: 1. liczba 2 jest pierwiastkiem wielomianu W(x)=x³−2x²−ax+1. Wyznacz a

Święty: W(2)=0 I rozwiązujesz rownanie z niewiadomą a

Mateusz: skoro 2 jest pierwiastkiem wielomianu to znaczy ze W(2)=0 a więc 2³−2*2²−a*2+1=0 rozwiązujesz takie rownanko

Sylwia: 2. a) rozwiąż równanie ^3x−9_x−3=2x b) Wykonaj działanie ²_2x−1 − ⁴_x−2 Wynik zapisz w najprostszej postaci.

Sylwia: 3. Oblicz: a) 2log₃27−log₂16 b) 2log₃6−log₃4

	320−319
c)
	318

d) sin²20⁰+sin²70⁰

Sylwia: 4. Wyznacz liczbę wyrazów ciągu a_n=−2n+100, które są ujemne.

Sylwia: 5. W ciągu arytmetycznym wyraz pierwszy jest równy −2, różnica tego ciągu jest równa 3. Oblicz, ile kolejnych początkowych wyrazów tego ciągu należy dodać, aby ich suma była równa 3575.

Sylwia: 6. Liczby 4, x−2, 9 tworzą w podanej kolejności ciąg geometryczny. Wyznacz x.

Sylwia: 7. Wiedząc, że cosα =0,6 i kąt α jest kątem ostrym, oblicz wartość pozostałych funkcji trygonometrycznych kąta α.

emagnuski: 3. Oblicz: a) 2log₃27−log₂16 = 2*3 − 4 = 6−4 = 2 b) 2log₃6−log₃4 = log₃6²−log₃4 = log₃36−log₃4 = log₃(36/4) = log₃9 = 2

Sylwia: 8. Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 220⁰. Oblicz miarę kąta środkowego

emagnuski: 3.

	320−319		318(32 − 3)
c)		=		= 32 − 3 = 9 − 3 = 6
	318		318

Alkain: zad 2. A) x≠3

3x−9		2x(x−3)
	−		=0
x−3		x−3

3x−9−2x2+6x
	=0
x−3

−2x2−3x−9
	=0
x−3

0 gdy −2x²+9x−9=0 Liczysz Δ i miejsca zerowe

Sylwia: 9. W okrąg wpisany jest kąt BAC równy 28⁰. Przez punkt C poprowadzono styczną do tego okręgu. Oblicz miarę kąta ostrego między tą styczną a cięciwą AC.

Alkain: zad.2 B

2		4
	−
2x−1		x−2

2(x−2)−4(2x−1)
(x−2)(2x−1)

2x−4−8x+4
2x2−x−4x+1

−6x
2x2−5x+1

Alkain: −2n+100<0 100<2n 50<n Dla n>50 ciąg przyjmuje wartości ujemne.

Alkain: Zad4 to wyżej oczywiście

Alkain: Zad.6 (x−2)²=4*9 x²−4x+4=36 x²−4x−32=0 Liczysz Δ i miejsca zerowe

emagnuski: Wiedząc, że cosα =0,6 i kąt α jest kątem ostrym, oblicz wartość pozostałych funkcji trygonometrycznych kąta α. sin²α+cos²α = 1 cos²α = (0,6)² = U{36/100} sin²α = 1−cos²α sin²α = 1−U{36/100} sin²α = U{64/100}

	8
sinα =
	10

sinα = 0,8

	sinα
tgα =
	cosα

	0,8		8		10		8		1
tgα =		=		*		=		= 1
	0,6		10		6		6		3

	1
ctgα =
	tgα

	1		6		3
ctgα =		=		=
	8   6		8		4

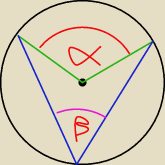
emagnuski: 8. Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 220. Oblicz miarę kąta środkowego α = 2β α+β = 220 => β=220−α Podstawiam do pierwszego wzoru: α = 2(220−α) α = 440 − 2α 3α = 440

	2
α = 146
	3

	2
β = 220 − 146
	3

	1
β = 73
	3

	2
Kąt środkowy to α = 146
	3

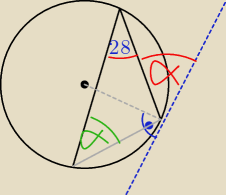
emagnuski: 9. W okrąg wpisany jest kąt BAC równy 28. Przez punkt C poprowadzono styczną do tego okręgu. Oblicz miarę kąta ostrego między tą styczną a cięciwą AC. Narysowałem, raczej tak to wygląda. Kąt na zielono ma raczej tą samą wartość co poszukiwany. Niestety nie bardzo wiem co robić z tym dalej.

Sylwia: dzięki i tak otrzymałam od Ciebie jak i innych ogromną pomoc

emagnuski: 5. W ciągu arytmetycznym wyraz pierwszy jest równy −2, różnica tego ciągu jest równa 3. Oblicz, ile kolejnych początkowych wyrazów tego ciągu należy dodać, aby ich suma była równa 3575. a₁ = −2 r = 3 n = ? S_n = 3575

	a1 + an
Sn =		n
	2

a_n = a₁+(n−1)r a_n = −2+(n−1)3 = −2+3n−3 = 3n − 5

	−2 + 3n − 5
Sn =		n
	2

	3n − 7
3575 =		n
	2

7150 = (3n − 7)n 7150 = 3n² − 7n 3n² − 7n − 7150 = 0 Δ = 49 + 85 800 = 85 849 = (√293)²

	7 − 293		−286		2
n1 =		=		= 47		− nie spełnia warunków zadania (n musi być
	6		6		3

całkowite)

	7 + 293		300
n2 =		=		= 50
	6		6

Odp. 50

komoo: ile punktow wspolnych ma okrag o rownaniu (x+2)2+(y−1)2=9

MQ: @komoo: zależy z czym

Marcin: https://matematykaszkolna.pl/forum/141364.html zerknie ktoś

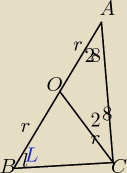
Jolanta: zad 9 rys. ten co u góry 1)Kat miedzy styczna do okręgu a cieciwa wychodząca z punktu styczności jest równy katowi wpisanemu opartemu na tej cieciwie Czyli dobrze emagnuski zaznaczył α 2)styczna jest prostopadła do promienia w obydwu trójkatach ramionami są promienie czyli trójkaty sa równoramienne OAC=ACO=28⁰ OAC=180⁰−2*28⁰=124⁰ OAB=180⁰ COB180⁰−124⁰=56⁰ OBC=BCO=(180⁰−56⁰):2=62⁰ α=62⁰

Brzuzia: Wiedząc, że cosα = 0,4 oblicz pozostałe funkcje trygonometryczne kąta α

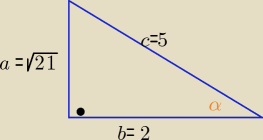
Eta: a>0 z tw. Pitagorasa a²=c²−b² ⇒ a= .... sinα=...... tgα=.... ctgα=...