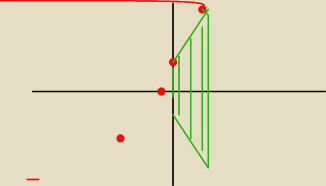
Objętość bryły - całki k123: Witam, oto rysunek. Bardzo proszę o pomoc, treść zadaniablicz objętość bryły powstałej przez obrót wokół osi OX A = {x,y}: 0< x <1 0 < y < x+ e^x a więc : V = π * ∫ (0,1) (x+e^x)² dx = π * [1/3 x³ + 2x−2e^x+e²x] (przedzial 0,1) Czy ja dobrze rozumiem zadanie, że: czerwona linia to y=x+e^x , więc bryła będzie wyglądać jak to zaznaczone na zielono? Chyba źle całki obliczyłam, ∫2xe^x i ∫ e²x , cos jest źle, bo nie wychodzi poprawny wynik (tzn π*( 0.5*e² + 5/6)) Bardzo proszę o pomoc

k123: dziwnie się zedytowało Czerwone kropki się nie połączyły, ale y=x+ e^x to połączenie ich

MQ: V=π∫₀¹(x+e^x)²dx=π∫₀¹(x²+2xe^x+e^2x)dx=π|¹₃x³+2xe^x−2e^x+¹₂e^2x|₀¹

k123: Dziekuje dokladnie tak ! Źle obliczyłam całke z e²x wlasciwie to nie weidzialam jak ja obliczyc Dziekuje !