trygonometria
asdf: Trygonometria
| | sinx | |
Ma ktoś zadania z trygonometrii? Udowodnij tożsamość, np. |
| = tgx itd.. |
| | cosx | |
10 kwi 21:00
Saizou :
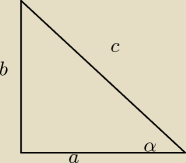
zatem
cnu.
10 kwi 21:04
10 kwi 21:06
Ajtek:
Takie coś, nie tyle udowodnij co sprawdź

.
(tg
2x−sin
2x)*ctg
2x=sin
2x
10 kwi 21:09
asdf: | | sin2 | | cos2 | | sin2(1 − cos2) | | cos2 | |
( |
| − sin2) * |
| = |
| * |
| = |
| | cos2 | | sin2 | | cos2 | | sin2 | |
| sin4 | | cos2 | | sin4cos2 | |
| * |
| = |
| = sin2 |
| cos2 | | sin2 | | sin2cos2 | |
L = P
10 kwi 21:59
asdf: 1 − U{sin2cos2}{sin2 = 1 − cos2 = sin2
10 kwi 22:00
Ajtek: Chcesz coś jeszcze?
10 kwi 22:00
asdf: Dzięki za zadania
1 = tg * ctg
−−−−−−−−−−−−−−−−−−−−−
| | sin2cos2 | |
1 − |
| = 1 − cos2 = sin2 |
| | sin2 | |
10 kwi 22:01
asdf: no dawaj

10 kwi 22:01
Ajtek: | | sinx | | 1 | |
ctgx+ |
| = |
| |
| | 1+cosx | | sinx | |
10 kwi 22:03
Ajtek: Masz jeszcze jeden:
cos
4x+sin
4x=1−2sin
2xcos
2x
do zrobienia w pamięci

.
10 kwi 22:06
asdf: sin
2 = 1 − cos
2
| cos | | sin | | cos(1 + cos) | | sin2 | |
| + |
| = |
| + |
| = |
| sin | | 1 + cos | | sin(1+cos) | | sin(1 + cos) | |
| cos + cos2 + sin2 | | cos + 1 | | 1 | |
| = |
| = |
| |
| sin + sincos | | sin(1 + cos) | | sin | |
more more more

10 kwi 22:09
asdf: a2 + b2 = 1
(a2 + b2)2 − 2(ab)2 = a4 + b4
10 kwi 22:17
Ajtek: Jedna uwaga nie możesz pisać sin, cos itd. bez argumentu! To jest
WIELBŁĄD.
Nawet tutaj, gdzie wiemy o co chodzi, po prostu nabierasz złych nawyków i to moze się kiedyś
obrócić przeciw Tobie (pisałem z rozpędu).
Masz jeszcze jeden do zrobienia w pamięci

.
10 kwi 22:19
Ajtek: O już zrobiłeś

.
10 kwi 22:19
Ajtek: | sinx | | 1+cosx | | 2 | |
| + |
| = |
| |
| 1+cosx | | sinx | | sinx | |
10 kwi 22:20
asdf: Wiem, tak normalnie to z kątem pisze.
10 kwi 22:21
Ajtek: I też sie przyczepię do rozwiązania.
NIe zapisałeś co to jest a
2 i b
2 
.
a=1, b=2 a
2+b
2≠1 i tyle!
10 kwi 22:22
10 kwi 22:24
asdf: | sinα | | 1α + cosα | |
| + |
| = |
| 1α + cosα | | sinα | |
| | sin2α | | (1α + cosα)2 | |
|
| + |
| |
| | sinα(1α + cosα) | | sinα(1α + cosα) | |
| | sin2α + 1α + 2cosα + cos2α | |
= |
| |
| | sinα(1α + cosα) | |
| | 2α(1α + cosα) | | 2α | |
= U {2α + 2cosα}{sinα(1α + cosα)} = |
| = |
| |
| | sinα(1α + cosα) | | sinα | |
P.S. Starczy tyle alfów?
10 kwi 22:26
Ajtek: a skąd 1α


10 kwi 22:29
asdf: a tak można zapisać

?
| ctgy + tgy | | tgy(c + 1) | | tgy | |
| = |
| = |
| |
| ctgx + tgx | | tgx(c + 1) | | tgx | |
coś mi nie wychodzi

10 kwi 22:30
asdf: Tak z rozpędu mi sie te alfy wcisnęły

hehe

10 kwi 22:31
Ajtek: Kombinuj

10 kwi 22:32
Ajtek: Popadasz ze skrajności w skrajność

.
10 kwi 22:32
asdf: zapisa taki:
tgy(c + 1) można pisać?

10 kwi 22:32
Ajtek: co to jest c?
10 kwi 22:35
asdf: tgy(
c + 1) =
ctgy + tgy


10 kwi 22:36
Ajtek: 
, wg mnie nie

10 kwi 22:36
Ajtek: Zauważ, iż tam masz dwa rózne kąty x i y!
10 kwi 22:37
asdf: to źle

10 kwi 22:37
asdf: tgx = ctgy?
10 kwi 22:37
Ajtek: NIe pamiętam

.
10 kwi 22:39
10 kwi 22:42
Ajtek: No coś w ten deseń

, czyli tylko w Δ prostokątnym

.
10 kwi 22:44
asdf:
| tgx + tgy | | | |
| = |
| = 1 |
| ctgx + ctgy | | | |
1 = tgx * ctgx ⇔ tgx * tgy

10 kwi 22:44
asdf: właśnie o takie zadania mi chodziło, masz jeszcze?
10 kwi 22:46
Ajtek: Rozwiązanie jest trochę bardziej zawiłe, sam je próbuję ogarnąc

.
10 kwi 22:49
DSGN.: | 1+sin4x | | 1+tg2x | |
| = |
| sprawdz tożsamosc  |
| cos4x | | 1−tg2x | |
10 kwi 22:49
Malwina: własnie nad jednym kombinuje
wykaż że jeśli sinα <
12 , to cos
2 α * tg
2α − cos
2 α < −
12
z chęcia zobacze cale rozwiazanie


10 kwi 22:49
Ajtek: Ale to nie jest poprawne

10 kwi 22:49
krystek: a na jakiej podstawie tgx*tgy=1? Przy jakim zał?
10 kwi 22:50
asdf: @
DSGN
tylko nie bardzo rozumiem sin
4x, ja dopiero w trygonometrii zaczynam a nie bardzo rozumiem
to

@
Ajtek Moje rozwiązanie jest nie poprawne?

@
Malwina
Zaraz też pokombinuje

10 kwi 22:52
asdf: @krystek, ze wzorów: tg * ctg = 1, a wyżej napisałeś założenie, do niego robiłem
10 kwi 22:54
krystek: Ale tgx*ctgx=1 Pomijasz argumenty!
10 kwi 22:56
asdf: nie bardzo Ciebie rozumiem, zrobiłem zadanie, według mnie jest dobrze, możesz mi to bardziej
wytłumaczyć czego brakuje

?
10 kwi 22:57
Ajtek: Nie jest poprawne
10 kwi 22:57
krystek: sin4x=sin[2(2x)]=2sin2x*cos2x
10 kwi 22:57
DSGN.:
oraz
| tg2x−sin2x | |
| =tg4x |
| 1−tg2xcosx | |
oraz
sinx*(sinx*tgx+cosx)=tgx
na początek takie ciekawsze

chyba ze chcesz jeszcze łatwiejsze

to cos poszukam

10 kwi 22:57
Basiek: | | 1 | |
wzór tgx*ctgx=tgx* |
| =1 i x=  |
| | tgx | |
A Ty....
| | 1 | |
|
| ≠1 |
| | tg | |
10 kwi 22:59
DSGN.: Basiek reaktywacja starego nicku?

10 kwi 23:00
Ajtek: DSGN zbiorek Dróbka Szymański

10 kwi 23:02
DSGN.: 22:42 Krystek napisał założenia dla równosci
10 kwi 23:02
Basiek: Pewien ktoś mi kazał.

Przepraszam, że tak się... wtrącam. Po prostu nauka czeka.

Mam nadzieję, że obrazowo to
przedstawiłam, mi zawsze pomaga.

10 kwi 23:02
DSGN.: Ajtek nie

Andrzej Kiełbasa

10 kwi 23:03
Ajtek: Aha, bo ja właśnie z tego zbiorku jadę, a te dwa przykłady są w tym samym zadaniu co mój tutaj
podany

10 kwi 23:04
asdf: @Basiek
Twój post z 22:59 nie jest taki sam jak mój z 22:44. Nie dopisywałem kątów przy sin i
cos. Uważam, że to zadanie jest dobrze zrobione.
Mogę to poprawić, jeżeli mnie nie zrozumieliście.
10 kwi 23:07
DSGN.: Dróbka Szymański robiłem tylko logarytmy

10 kwi 23:08
Ajtek: Heh, ja podczas świątecznych porządków znalazłem wydanie z 1976 roku

.
10 kwi 23:09
Basiek: Łapię, aż do tego momentu:
1 = tgx * ctgx ⇔ tgx * tgy <− że niby co?
"Jeden jest równe tgx*ctgx wtedy i tylko wtedy, gdy tgx*tg
co?"
No i nie odnosiłam się nijak do 22:44, tylko troszkę później... , ale to już mniejsza.

10 kwi 23:11
krystek: I to wydanie IV −te?
10 kwi 23:11
Ajtek: Tak, dla klasy I i II L.O. Cena na okładce 16 zł

10 kwi 23:12
DSGN.: ja mam wydanie XX rok 96

10 kwi 23:13
asdf: tgx = ctgy
tgy = ctgx
1 = tgx * tgy = tgx * ctgx, tak o powinno być, może źle zinterpretowałem znak.
10 kwi 23:14
krystek: I okładka granatowa −pozdrawiam
@AjtekWprowadź asgf na własciwe tory myslenia!
10 kwi 23:14
Ajtek: Dokładnie, z jasnozielonym grafem na okładce.
Z tym wprowadzeniem na tory myślenia to dzisiaj bedzie problem, gdyż nie do końca łapię
podpowiedź w rozwiązaniu, zmęczenie daje znać o sobie

.
10 kwi 23:18
Basiek: Dobra, ze mną coś jest chyba już mocno nie tak.
tgy=ctgx?
A niby z jakiej okazji? To jest trójkąt prostokątny?
10 kwi 23:19
asdf: @Basiek
Nie chcę się kłócić, ale w podstawach programowych z matematyki podstawowej dla szkół
ponadgimnazjalnych w dziale trygonometria nie ma innych trójkątów jak prostokątne.
10 kwi 23:22
krystek: To wtedy x+y=90 .
A Ty chciałeś miec tożsamości . A to winno brzmiec : wykaz ,że tgx*ctgy=1
10 kwi 23:27
asdf: To może mi ktoś napisać rozwiązanie do tego zadania?
10 kwi 23:28
Eta:
| | 1−tg2x | |
1/ |
| = 1−2sin2x cos2x ≠0 |
| | 1+tg2x | |
mnożąc licznik i mianownik przez cos
2x
| | cos2x−sin2x | | 1−2sin2x | |
L= |
| = |
| = 1−2sin2x |
| | cos2x+sin2x | | 1 | |
L=P
10 kwi 23:28
Basiek: Ja właśnie... czegoś tu nie rozumiem.
Żeby tak rozwiązywać te tożsamości, musiałby być dopisek "W trójkącie prostokątnym, w którym
kąty ostre mają miary x i y zachodzi równość ... (tu tożsamość)...., udowodnij, że jest ona
prawdziwa"

Chyba.
10 kwi 23:29
Eta:
Dokładnie tak ...........


10 kwi 23:31
Ajtek: No włąśnie o to chodzi. W roku 1976 nie było ograniczeń typu x+y=90. Matma była na zupełnie
innym poziomie. Dla dzisiejszych maturzystów, nawet z rozszerzenia, poziom to kosmiczny
wręcz.
10 kwi 23:32
Basiek: Ech, ale jak już robimy takie porównania...
na wielu uczelniach technicznych przelicznik punktów z matury
geografia= matematyka.
Napisanie rozsz. geografii na 80% + to kwestia nauki 1,5−2 mies., no trzeba się obkuć, nie
przeczę. Napisanie tak matematyki....
No właśnie. Chyba większość porównań traci sens w szerszym zestawieniu

10 kwi 23:34
DSGN.: i tu sie
Basiek z Tb zgodzę moja kolezanka przeczytała dokładnie vademecum z geografii
i napisała własnie R na jakieś ponad 80(cos) a matematykę R gdzie tez solidnie sie uczy 12%
ale to jest ta połowa co odpada na 1 roku bo nie radzi sb z matmą


10 kwi 23:40

 .
(tg2x−sin2x)*ctg2x=sin2x
.
(tg2x−sin2x)*ctg2x=sin2x

 .
.


 .
.
 .
.
 .
a=1, b=2 a2+b2≠1 i tyle!
.
a=1, b=2 a2+b2≠1 i tyle!


 ?
?

 hehe
hehe 

 .
.



 , wg mnie nie
, wg mnie nie 

 .
.
 , czyli tylko w Δ prostokątnym
, czyli tylko w Δ prostokątnym  .
.

 .
.




 @Ajtek Moje rozwiązanie jest nie poprawne?
@Ajtek Moje rozwiązanie jest nie poprawne?  @Malwina
Zaraz też pokombinuje
@Malwina
Zaraz też pokombinuje 
 ?
?
 chyba ze chcesz jeszcze łatwiejsze
chyba ze chcesz jeszcze łatwiejsze  to cos poszukam
to cos poszukam 

 * ctg
* ctg = tg
= tg *
*


 Przepraszam, że tak się... wtrącam. Po prostu nauka czeka.
Przepraszam, że tak się... wtrącam. Po prostu nauka czeka.  Mam nadzieję, że obrazowo to
przedstawiłam, mi zawsze pomaga.
Mam nadzieję, że obrazowo to
przedstawiłam, mi zawsze pomaga. 
 Andrzej Kiełbasa
Andrzej Kiełbasa 


 .
.



 .
.
 Chyba.
Chyba.




