proszę o pomoc maturzysta: Udowodnij,że dla dowolnego trójkąta prostokątnego o przyprostokątnych długości a i b oraz przeciwprostokątnej długości c:

	a+b−c
a) promień okręgu wpisanego w ten trójkąt wyraża się wzorem r=
	2

b) suma średnic okręgu wpisanego i opisanego na tym trójkącie jest równa sumie długości jego przyprostokątnych c)wysokość poprowadzona z wierzchołka kąta prostego jest średnią geometryczną długości odcinków, na jakie ta wysokość podzieliła przeciwprostokątną d) suma kwadratów sinusów miar wszystkich kątów wewnętrznych tego trójkąta jest równa 2

Eta: maturzysto nie czekaj na gotowce ( to łatwe dowody ) Poszukaj w postach! Było 1000 razy

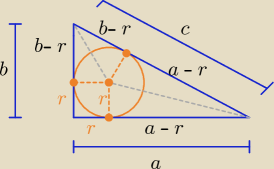
Eta: 1/

	a+b−c
c=a−r+b−r ⇒ 2r=a+b−c r=
	2

	1
2/ R=		c ⇒ 2R=c
	2

2r=a+b−2R ⇒ 2r+2R=a+b

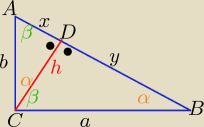
Eta: c) ΔCDB ~ ΔCDA to:

	x		h
		=		⇒ h2=x*y
	h		y

Eta: d) udowodnij samodzielnie sin²α+sin²β+ sin²90^o= ..........

maturzysta: Nie wiem jak udowodnić to d.

Eta: Ejjj sinβ= cosα sin90^o=1 sin²α+cos²α+sin²90^o= 1+1= ? ( wiesz ile jest 1+1 ?

maturzysta: Rzeczywiście proste, ale samemu cieżko wpaść. Dzięki wielkie.

Eta: