pomocy prosze
Betkaa:
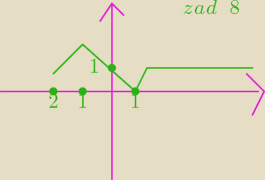
zad8 Dana jest funkcja y=f(x) wykresem funkcji y=f(x+1) jest :
dlaczego taki rysunek

zad 14 prosta równoległa do prostej y=−2x+3 i przechodząca przez punkt {=(1,2) ma równanie
zad16 równanie okręgu o środku S=(1,2) przechodzącego przez punkt A=(3,3) ma postać:
zad 18 sciana boczna ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości a=6cm
tworzy z płaszczyzną podstawy kat α=60 stopni wysokośc ostrosłupa ma długośc?
10 kwi 17:13
emagnuski: Zad 14
Zmienną a1 bierzemy z pierwotnej funkcji, czyli a1 = −2
A więc mamy już funkcję w postaci:
y2 = −2x + b
Do tego wzoru podstawiamy dane punktu:
2 = −2*1 + b
Wyliczamy b:
b = 4
czyli:
y2 = −2x + 4
Sprawdzenie poprzez podstawienie punktu do wzoru końcowego:
y2 = −2*1 + 4
y2 = 2
Czyli zgadza się.
10 kwi 17:23
Jack:
f(x+1), to przesunięcie funkcji f(x) o jedną jednostkę w lewo.
10 kwi 17:24
emagnuski:
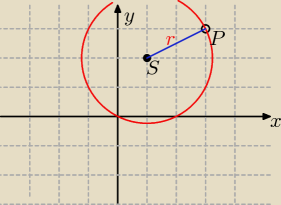
Zad. 16
Wzór ogólny na okrąg to:
(x − x
0)
2 + (y − y
0)
2 = r
2
S = (1,2) = (x
0, y
0)
Promień r obliczamy z tw. Pitagorasa:
r
2 = 2
2 + 1
2
r
2 = 4 + 1
r
2 = 5
r =
√5
Mamy wszystkie dane, można je podstawić do wzoru ogólnego:
(x − 1)
2 + (y − 2)
2 = 5
10 kwi 17:34
Betkaa: dziękuje!

10 kwi 17:35
Betkaa: a 18 juz zrobiłam wiec juz nie chce

dzięki za pomoc

10 kwi 17:40
emagnuski:
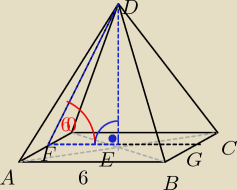
Zad 18
Do obliczenia wysokości należy wykorzystać prostokątny trójkąt DEF
|FG| = |AB| = 6
|FE| =
|FG|2 =
62 = 3
tg60 =
|DE||FE|
|DE| = |FE|tg60
|DE| = 3*
√3
H = |DE| = 3
√3
Wysokość jest równa 3
√3
10 kwi 17:44
emagnuski: Za późno, już zrobiłem.

10 kwi 17:46
bussiaa: to dziekuje wyszlo mi podobnie

ale przepisze tez twój sposób bo cos mi w moim nie pasuje hehe

10 kwi 17:53
 zad8 Dana jest funkcja y=f(x) wykresem funkcji y=f(x+1) jest :
dlaczego taki rysunek
zad8 Dana jest funkcja y=f(x) wykresem funkcji y=f(x+1) jest :
dlaczego taki rysunek zad 14 prosta równoległa do prostej y=−2x+3 i przechodząca przez punkt {=(1,2) ma równanie
zad16 równanie okręgu o środku S=(1,2) przechodzącego przez punkt A=(3,3) ma postać:
zad 18 sciana boczna ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości a=6cm
tworzy z płaszczyzną podstawy kat α=60 stopni wysokośc ostrosłupa ma długośc?
zad 14 prosta równoległa do prostej y=−2x+3 i przechodząca przez punkt {=(1,2) ma równanie
zad16 równanie okręgu o środku S=(1,2) przechodzącego przez punkt A=(3,3) ma postać:
zad 18 sciana boczna ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości a=6cm
tworzy z płaszczyzną podstawy kat α=60 stopni wysokośc ostrosłupa ma długośc?
 Zad. 16
Wzór ogólny na okrąg to:
(x − x0)2 + (y − y0)2 = r2
S = (1,2) = (x0, y0)
Promień r obliczamy z tw. Pitagorasa:
r2 = 22 + 12
r2 = 4 + 1
r2 = 5
r = √5
Mamy wszystkie dane, można je podstawić do wzoru ogólnego:
(x − 1)2 + (y − 2)2 = 5
Zad. 16
Wzór ogólny na okrąg to:
(x − x0)2 + (y − y0)2 = r2
S = (1,2) = (x0, y0)
Promień r obliczamy z tw. Pitagorasa:
r2 = 22 + 12
r2 = 4 + 1
r2 = 5
r = √5
Mamy wszystkie dane, można je podstawić do wzoru ogólnego:
(x − 1)2 + (y − 2)2 = 5

 dzięki za pomoc
dzięki za pomoc 
 Zad 18
Do obliczenia wysokości należy wykorzystać prostokątny trójkąt DEF
|FG| = |AB| = 6
|FE| = |FG|2 = 62 = 3
tg60 = |DE||FE|
|DE| = |FE|tg60
|DE| = 3*√3
H = |DE| = 3√3
Wysokość jest równa 3√3
Zad 18
Do obliczenia wysokości należy wykorzystać prostokątny trójkąt DEF
|FG| = |AB| = 6
|FE| = |FG|2 = 62 = 3
tg60 = |DE||FE|
|DE| = |FE|tg60
|DE| = 3*√3
H = |DE| = 3√3
Wysokość jest równa 3√3

 ale przepisze tez twój sposób bo cos mi w moim nie pasuje hehe
ale przepisze tez twój sposób bo cos mi w moim nie pasuje hehe 