Proszę o pomoc Adam: Wyznacz liczbę rozwiązań równania a²+||x+1|−1|=1 w zależności od parametru m.

Adam: znaczy a

rumpek: Narysować wykres ||x + 1| − 1| potem odczytać tylko w zależności od parametru i otrzymane rozwiązania skonsultować z warunkiem 1 − a²

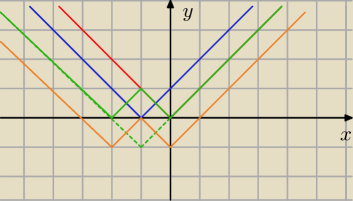
rumpek: * czerwony to wykres |x| * niebieski to wykres |x + 1| * zielony to wykres ||x + 1| − 1| * pomarańczowy to wykres ||x + 1| − 1| − 1 teraz tylko odczytać

Adam: coś mi nie wychodzi za bardzo

Adam: a jak będzie wyglądać wykres −a²?

rumpek: tam jest a, czy a²? bo w poście z 16:02 napisałeś a WYKRESU a² nie rysujemy

Adam: znaczy a² przepraszam, a to coś zmienia?

Adam: czyli źle?

rumpek: To teraz ||x + 1| − 1 | −1 = −a² * 0 rozwiązań dla −a² < −1 ⇒ a∊ ... * 2 rozwiązania dla −a² > 0 ⇒ a∊ ... * 2 rozwiązania dla −a² = −1 ⇒ a∊ ... * 3 rozwiązania dla −a² = 0 ⇒ a∊ ... * 4 rozwiązania − 1 < −a² < 0 ⇒ a∊ ... Dalej sam pomyśl Jak pozbyć się tych kwadratów

pigor: ... otóż, np. tak : a²+||x+1|−1|=1 ⇔ ⇔ ||x+1|−1|=1−a² i 1−a² ≥0, czyli a²≤ 1 ⇔ |a|≤ 1 ⇔ −1≤ a≤ 1 , a więc mając wykres funkcji y=||x+1|−1| i warunek −1≤ a≤ 1 , łatwo stwierdzić (odczytać z wykresu) , że liczba pierwiastków jako np.funkcja p(a) ma postać : 0 gdy −1≤ a< 0 , p(a) = 2 gdy a=0 , 4 gdy 0< a<1 , 3 gdy a=1 . ...

Adam: dziękuję za pomoc