Witam :)
Bartek.: Witam

1. W Okrąg o promieniu 5 cm wpisano trapez tak, że jedna z podstaw jest średnicą okręgu. Oblicz
obwód tego trapezu wiedząc, że jego przekątna tworzy z dłuższa podstawą kąt o mierze 30 st.
10 kwi 11:51
krystek:
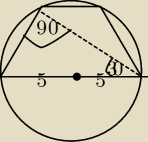
10 kwi 11:54
Bartek.: no tak, czyli mamy tr.o katach 30 i 60 st., trapez jest równoramienny. dolna podstawa 10 cm,
katy rozwarte po 120 st. ale jak obliczyć długości ramion?
10 kwi 12:02
krystek: | | r | |
funkcje trygonometryczne |
| =... |
| | 10 | |
10 kwi 12:05
Bartek.: czyli jedno ramię 5 cm?
10 kwi 12:26
rumpek: 
10 kwi 12:27
Bartek.: nie miałem jeszcze tych funkcji trygonometrycznych, ale jeżeli środek okręgu połączę z
wierzchołkiem to powstanie tr. równoramienny a podstawie 5 cm , więc każdy bok będzie miał 5
cm. więc krótsza podstawa też powinna mieć 5 cm ?
10 kwi 12:29
rumpek:
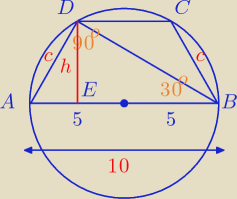
Zauważ, że pole trójkąta ABD możemy obliczyć na dwa sposoby

1
o
c = 5
2
o
c
2 + |BD|
2 = 10
2
25 + |BD|
2 = 100
|BD|
2 = 75, |BD| ∊ R
+
|BD| =
√75 = 5
√3
3
o
| | 1 | | 1 | |
P△ABD = |
| * c * |BD| = |
| * 10 * h |
| | 2 | | 2 | |
| 1 | | 1 | |
| * 5 * 5√3 = |
| * 10 * h |
| 2 | | 2 | |
25
√3 = 10h / : 10
4
o Obliczmy teraz odcinek |AE|
h
2 + |AE|
2 = c
2
5
o
|DC| = 10 − 2 * |AE|
|DC| = 10 − 5 =
5
6
o
L = 2 * 5 + 5 + 10 = 10 + 15 = 25

10 kwi 12:37
pigor: ...
Bartku rozumujesz sam b. dobrze i nie bierz czasem przykładu z rozwiązania
powyżej , bo zadanie rozwiązuje się ... w pamięci z własności trójkąta prostokątnego
ekierki (90
o,60
o,30
o) i tyle , pozdrawiam , tak trzymaj

. ...

10 kwi 12:52
Bartek.: no w sumie to myślę, ze jak podzielę ten trapez na trzy tr. równoramienne to otrzymam ten sam
wynik..

10 kwi 12:56
Bartek.: równoboczne *
10 kwi 13:04
pigor: ... myślę, że chciałeś powiedzieć więcej

, bo równoboczne , prawda

. ...

10 kwi 13:04
pigor: ... O! miałem rację ...

co myślałeś i pozdrawiam jeszcze raz .
10 kwi 13:06
Bartek.: dzięki wszystkim i również pozdrawiam

10 kwi 13:14
 1. W Okrąg o promieniu 5 cm wpisano trapez tak, że jedna z podstaw jest średnicą okręgu. Oblicz
obwód tego trapezu wiedząc, że jego przekątna tworzy z dłuższa podstawą kąt o mierze 30 st.
1. W Okrąg o promieniu 5 cm wpisano trapez tak, że jedna z podstaw jest średnicą okręgu. Oblicz
obwód tego trapezu wiedząc, że jego przekątna tworzy z dłuższa podstawą kąt o mierze 30 st.


 Zauważ, że pole trójkąta ABD możemy obliczyć na dwa sposoby
Zauważ, że pole trójkąta ABD możemy obliczyć na dwa sposoby  1o
1o

 . ...
. ... 

 , bo równoboczne , prawda
, bo równoboczne , prawda  . ...
. ... 
 co myślałeś i pozdrawiam jeszcze raz .
co myślałeś i pozdrawiam jeszcze raz .
