Równanie okręgu
gallanonim: Napisz równanie okręgu o środku w punkcie A(3,−1) i promieniu r=∫2
a)czy punkt P(2,0) należy do tego okręgu?
Narysuj.
10 kwi 11:19
kam: a tam masz pierwiasek z 2 r czy 2?
10 kwi 11:22
gallanonim: pierwiastek z dwóch
10 kwi 11:24
krystek: (x−3)2+(y+1)2=r2 (nie wiem ile jest r=?)
i wstaw teraz wsp punktu A lub rysujesz okrąg i zobaczysz .
10 kwi 11:25
gallanonim: r nie bylo podane w zadaniu
10 kwi 11:28
gallanonim: gdzie te współrzędne mam wstawic? nie mam bladego pojecia o co chodzi
10 kwi 11:29
krystek: Do równania okręgu!
10 kwi 11:32
krystek:
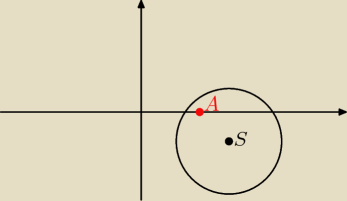
10 kwi 11:40
kam:
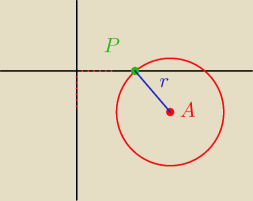
(x−3)
2 + (y+1)
2 = 2
środek okręgu A = (3, −1) promień r=
√2
P= (2;0)
teraz wstaw punkt P do równania i wyjdzie (2−3)
2 + (0+1)
2 = 2
1+1 = 2
⇒ L= P czyli punkt należy do okregu
lub
odległość punktu P od środka powinna wynosić tyle co promień czyli |PA| = r =
√2
|PA| =
√(2−3)2 + (−1−0)2 =
√2
√(−1)2 + (−1)2 =
√2
√1+1 =
√2
√2 =
√2 ⇒L=P czyli punkt nalezy do okregu
**
√2 to ok 1,4 → do rysunku, czyli ok 1,4 kratki
10 kwi 11:45
10 kwi 11:58
