.
Kasia: Witam.
Bardzo proszę o pomoc w rozwiązaniu dwóch zadań, najbardziej zalezy mi na poprawnych rysunkach
i jakichs podpowiedziach, ktore by mi pomogly wpasc na dobra droge

z góry dziekuje!
1. Oblicz pole powierzchni calkowitej i objetosc prawidlowego graniastoslupa czworokatnego,
ktorego przekatna ma dlugosc 14 cm oraz:
a) kat miedzy ta przekatna a przekatna sciany bocznej wychodzacymi z tego samego wierzcholka ma
30 stopni.
2. Pole powierzchni calkowitej prostopadloscianu wynosi 50(1+2
√3) cm
2. Przekatna jednej ze
scian bocznych jest nachylona do plaszczyzny podstawy pod katem 45 stopni, a przekatna
sasiedniej sciany bocznej jest nachylona do plaszczyzny podstawy pod katem 60 stopni. Oblicz
dlugosci krawedzi tego prostopadloscianu.
10 kwi 00:57
Buuu:
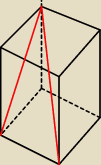
Z własności trójkąta 30−60−90 obliczasz długość przkątnej ściany bocznej oraz długość krawędzi
podstawy. Mając te dane obliczasz wysokość prostopadłościanu.
10 kwi 01:11
Buuu:
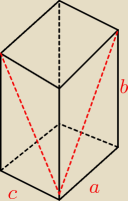
Boki a i b mają tą samą długość (a). Z własności trójkąta 3−6−9 można wywnioskować, że wysokość
| | a√3 | |
a=c√3, zatem c = |
| . Ostatetcznie wymiary prostopadłościanu to: |
| | 3 | |
10 kwi 01:18
Kasia: mam pytanie co do 1. zadania. W ktorym miejscu tworzy sie kat prosty? bo nie za bardzo to widze
czy to ten na prawo czy na lewo.
i co do 2. zadanka. nie rozumiem skd sie wzielo a = c√3 , z jakiego wzorku i konkretnie na
podstawie czego to wynika?
10 kwi 10:12
Kasia: hm?
10 kwi 10:22
krystek:
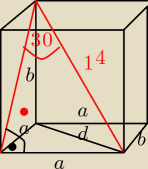
10 kwi 10:32
Kasia: nie wiem jak to widzicie, ale uwierze na słowo, że tam jest.. czyli przekatna tej sciany
bocznej (po lewej stronie) jest w tym przypadku wysokoscia tego trojkata rownobocznego, ktory
sie tworzy z tak jakby przedluzenia tego trojkata 30,60,90? i a = 7 tak?
10 kwi 10:36
10 kwi 10:38
Kasia: ok, to już rozumiem

a móglbys mi odpowiedziec na moje pytanko dotyczace 2. zadanka? z góry
dziekuje

10 kwi 10:48
krystek:
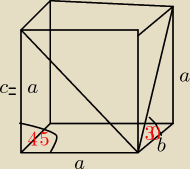
10 kwi 10:55
krystek: | | a | | b | |
Pc=2*a2+4a*b i teraz |
| =tg30 lub |
| =ctg30 |
| | b | | a | |
10 kwi 10:59
Kasia: krystek, powiedz mi czy gdzies sie pomylilam czy cos, bo raczej wynik nie bedzie sie zgadzal z
odpowiedziami. Z 1. zadania a=7 i H wyszlo mi
√24,5 , czy cos nie tak?
co do 2. tam kat drugi mial miec 60 stopni, ale to nie ma problemu. tylko,ze przy wyliczaniu b
i przekatnej sciany bocznej (tej prawej) wychodza mi jakies glupoty. Bo to a w tej scianie
bocznej jest wysokoscia trojkata rownobocznego (po dorysowaniu drugiej czesci trojkata). wiec
podstawilam sobie do wzoru na wysokosc (zeby wyliczyc najpierw przekatna tej sciany bocznej
| | a√3 | |
prawej, a pozniej b to bylaby po prostu polowka tej przekatnej). a = |
| i w ogole |
| | 2 | |
sie a skraca.. wiec jak to mam wyliczyc? prosze pomoz..
10 kwi 11:13
Kasia: z tych tg i ctg wyszlo mi ze b = √3a faktycznie.. ale dlaczego mi nie wychodzilo za pomoca
wzoru na wysokosc, co nie tak?
10 kwi 11:18
Kasia: ale chwila chwila, zle.. tam powinien byc tg60, a nie tg30stopni, czyz nie?
10 kwi 11:22
krystek: Widocznie wzięłaś złe zależności, lepiej licz funkcjami tryg, mniejsze prawdopodobieństwo
popełnienia błędu.
Zad 1 nie liczę podaję wskazówki.
10 kwi 11:22
Kasia: ale niestety nie wychodzi mi jak w odp i nie wiem co zle zrobilam.. ( co do 1. zadania)
10 kwi 11:25
krystek: Zapisz sprawdzę .
10 kwi 11:32
Kasia: a=7
| | 7√3 | |
d (przekatna sciany bocznej) = |
|
|
| | 2 | |
pozniej narysowalam sobie na boku trojkat prostokatny z H, d i a
z Pitagorasa
H
2 = 24,5
H =
√24,5
10 kwi 11:38
krystek: d=7
√3] poniieważ U{d}[14=cos30
10 kwi 11:44
krystek: miało być wyżej d=7√3 ponieważ:
10 kwi 11:45
krystek:
10 kwi 11:45
Kasia: okej, już widzę błąd, dziękuję

nie no ja już powariuje z tym drugim zadankiem, kompletne bzdury mi wychodzą, mogę zaraz
zapisac i sam/a zobaczysz, ze guzik z tego

10 kwi 11:47
krystek: ok
10 kwi 11:51
Kasia: b
√3= a
Pc = 2a
2 + 4ab
| | √3a | |
50+ 100√3 = 2a2 + 4a* |
| / *3
|
| | 3 | |
150 + 300
√3 = 6a
2 + 4a
√3a
i juz z tego chyba sie nie wybrnie.. cos jest nie tak, a nie wiem co, wszystko wydaje sie ok..
10 kwi 11:54
krystek: Po prawej stronie masz 4a2√3 i a2 przed nawias lub za a wcześniej podstawiasz bp{3]
10 kwi 12:00
Kasia: fakt

| | 150+300√3 | |
doszłam do postaci a2 = |
| i coś utknęłam..
|
| | 6+4√3 | |
probowalam wylaczyc
√3 przed nawias jednak to na dluzsza mete nie skutkuje bo i tak ciagle
| | 150 | |
zostaje gdzies ten pierwiastek.. czy moge rozbic ten ulamek na dwa czyli |
| + |
| | 6 | |
| | 300√3 | |
|
| czy nie wolno tak robic? |
| | 4√3 | |
10 kwi 12:06
krystek: Nie ! natomiast wcześniej skróć przez dwa i usuń niewymierność
10 kwi 12:11
10 kwi 12:13
Kasia: wyciagnelam 2 przed nawias i skrocilam i mam postać
i teraz mam zarowno licznik jak i mianownik pomnoizyc przed (3−2
√3) tak?
10 kwi 12:16
Kasia: okeej okej , już wyliczam

10 kwi 12:16
Kasia: doszlam do postaci
a2 = −75 − 50√3
nie wiem jak z tego teraz ma mi wyjsc a = 5 (co by sie zgadzalo z odpowiedzia).. cos dziwne..
jesli uwazasz,ze jest nie tak to podam wczesniejsze obliczenia
10 kwi 12:22
krystek: | | 75((1+2√3)(3−2√3 | |
a2= |
| |
| | (3−2√3)(3+2√3) | |
10 kwi 12:23
krystek: Z tego a nie wyjdzie=5 Później przeliczę − teraz wychodzę!
10 kwi 12:24
Kasia: no wiem wlasnie.. okej, dziękuję bardzo! : )
10 kwi 12:25
krystek: Kasiu ,aby wynik dla a =5 to w zadaniu winnas mieć Pc=50(3+2√3)
10 kwi 17:41
Kasia: jednak Pc jest takie jakie podalam.. chcesz zasugerowac,ze jest bład w tresci?
10 kwi 22:18
krystek: Po wyprowadzeniu wzoru
Pc=2a2(2√3+3) otrzymujemy i przyrównując do podanej wartości nie otrzymasz − jak wcześniej
pisałaś a=5
10 kwi 22:31
 z góry dziekuje!
1. Oblicz pole powierzchni calkowitej i objetosc prawidlowego graniastoslupa czworokatnego,
ktorego przekatna ma dlugosc 14 cm oraz:
a) kat miedzy ta przekatna a przekatna sciany bocznej wychodzacymi z tego samego wierzcholka ma
30 stopni.
2. Pole powierzchni calkowitej prostopadloscianu wynosi 50(1+2√3) cm2. Przekatna jednej ze
scian bocznych jest nachylona do plaszczyzny podstawy pod katem 45 stopni, a przekatna
sasiedniej sciany bocznej jest nachylona do plaszczyzny podstawy pod katem 60 stopni. Oblicz
dlugosci krawedzi tego prostopadloscianu.
z góry dziekuje!
1. Oblicz pole powierzchni calkowitej i objetosc prawidlowego graniastoslupa czworokatnego,
ktorego przekatna ma dlugosc 14 cm oraz:
a) kat miedzy ta przekatna a przekatna sciany bocznej wychodzacymi z tego samego wierzcholka ma
30 stopni.
2. Pole powierzchni calkowitej prostopadloscianu wynosi 50(1+2√3) cm2. Przekatna jednej ze
scian bocznych jest nachylona do plaszczyzny podstawy pod katem 45 stopni, a przekatna
sasiedniej sciany bocznej jest nachylona do plaszczyzny podstawy pod katem 60 stopni. Oblicz
dlugosci krawedzi tego prostopadloscianu.
 Z własności trójkąta 30−60−90 obliczasz długość przkątnej ściany bocznej oraz długość krawędzi
podstawy. Mając te dane obliczasz wysokość prostopadłościanu.
Z własności trójkąta 30−60−90 obliczasz długość przkątnej ściany bocznej oraz długość krawędzi
podstawy. Mając te dane obliczasz wysokość prostopadłościanu.
 Boki a i b mają tą samą długość (a). Z własności trójkąta 3−6−9 można wywnioskować, że wysokość
Boki a i b mają tą samą długość (a). Z własności trójkąta 3−6−9 można wywnioskować, że wysokość

 a móglbys mi odpowiedziec na moje pytanko dotyczace 2. zadanka? z góry
dziekuje
a móglbys mi odpowiedziec na moje pytanko dotyczace 2. zadanka? z góry
dziekuje

 nie no ja już powariuje z tym drugim zadankiem, kompletne bzdury mi wychodzą, mogę zaraz
zapisac i sam/a zobaczysz, ze guzik z tego
nie no ja już powariuje z tym drugim zadankiem, kompletne bzdury mi wychodzą, mogę zaraz
zapisac i sam/a zobaczysz, ze guzik z tego

