Największe paradoksy obecnej podstawy programowej Gustlik: Największe paradoksy obecnej podstawy programowej z matematyki: 1. Przeniesienie na poziom rozszerzony dzielenia wielomianów, schematu Hornera oraz twierdzenia Bezout, czyli PODSTAWOWYCH i najważniejszych metod rozkładu wielomianów na czynniki, na poziomie podstawowym tego nie ma, a metoda ta nie jest skomplikowana, 2. Przeniesienie na poziom rozszerzony rachunku wektorowego, który jest PODSTAWĄ geometrii analitycznej, jest przy tym prosty i znacznie skraca i ułatwia rozwiązywanie wielu zadań z tego działu, 3. Rachunek prawdopodobieństwa − tu już totalny bajzel. Nie dość, że przeniesiono na poziom rozszerzony kombinatorykę, która jest PODSTAWĄ rachunku prawdopodobieństwa, to do tego zastąpiono ją metodą drzewek. A metoda drzewek to nic innego, jak prawdopodobieństwo całkowite, które pod tą nazwą zostało usunięte całkowicie z programu, nawet z rozszerzeń. Wprowadzono więc drzewka nie wyjaśniając, skąd się one wzięły. Czyli na podstawach proste zadania typowo kombinatoryczne, jak np. rzut dwiema kostkami czy losowanie trzech kart z talii robi się drzewkami, czyli prawdopodobieństwem całkowitym, i trwa to ze trzy razy dłużej, niż kombinatoryką. W dodatku w większości działów zauważyłem, że wiele fajnych, prostych i ciekawych metod zostało przeniesionych na rozszerzenie albo w ogóle usuniętych z programu nauczania w szkole średniej. Natomiast zadania, w których te usunięte metody znacznie uprościłyby ich rozwiązywanie, rozwiązuje sę metodami "dookoła świata", bo trzeba pominąć usunięte wzory, po co je wprowadzać. Uczniowie skarżą się, że na rozszerzeniach te same zadania rozwiązuje się prostszymi metodami, niż na podstawach, i niestety mają 100 % racji. Skarżą się również rodzice, którzy chcieliby pomóc swoim dzieciom, ale nie dają rady, bo nie znają tych nowych pokręconych metod i chcieliby rozwiazać zadania "starymi", prostszymi metodami. Lepiej zrobić uczniom mętlik w głowie rozwiązując pięć układów równań, zamiast wprowadzić prosty wzór i zrobic zadanie w trzech linijkach. Efekt − 21 % oblanych matur z matematyki w roku 2011 w maju. Jestem przekonany, że co najmniej połowa tych oblanych matur to wina spapranego programu nauczania i topornej metodyki, stosowanej przez większość nauczycieli. Mamy więc podstawy bez podstaw − szczerze mówiąc − nie kumam, o co tutaj chodzi.

Kasia: Jako tegoroczna maturzystka w 100% się zgadzam. Widzę po swoich znajomych ile osób musi brać korepetycje, bo na lekcji rozwiązuje się często zadania jakimiś mega długimi sposobami, mimo iż faktycznie poznając jedną prostą własność, wzór, można go zrobić 2,3 razy szybciej.. i niestety przez to tyle osób nie próbuje nawet polubić matematyki widząc całą tablicę obliczeń i oczywiście zbyt wielkiego wytłumaczenia nie ma, słyszy się tylko: wyprowadzenie jest na rozszerzeniu, to po prostu musicie zapamiętać itd itd. Z matematyki robi się PAMIĘCIÓWKĘ, a to nie na tym polega.. i przedmiot ten traci cały swój urok.. Mam nadzieję, że to się z czasem zmieni i będzie zmierzać ku lepszemu, bo jak na razie to jak wyglądają lekcje matematyki (mówię o podstawie) to jest często śmiech na sali..

Gustlik: No właśnie, na podstawie jest najgorzej. Ja dlatego uczę rozszerzeń, bo inaczej to droga przez mękę. Nie rozumiem postępowania nauczycieli, przecież nikt im nie zabrania rozszerzać programu i wprowadzać prostszych metod, wręcz przeciwnie MEN i CKE są za tym, żeby nauczyciele uczyli więcej, niż wymaga tego podstawa programowa. Dlatego wszystkim maturzystom radzę, aby uczyli się wg "mojego" programu nauczania zamieszczonego w każdym dziale w komentarzach. Program ten w większości bazuje na starym, sprawdzonym programie nauczania matematyki i uczenie się wg niego daje niemal 100% gwarancję zdania matury.

Kasia: Dokładnie. Niestety obawiam się, że na przeszkodzie tu stoi ciągły brak czasu.. Choć z drugiej strony gdyby tak zliczyć ilość zmarnowanego czasu na rozwiązywaniu nie raz jednego zadania przez 30 minut, to wyjdzie na to, że w tym czasie zdążyłoby się już rozszerzyć ciut materiał i zrobić szybszym sposobem.. Jak widać niestety prawie nikomu się tego nie chce robić, bo i po co.. niech później będą słabe oceny ze sprawdzianów, zniechęcenie do przedmiotu. Pewnie. Tak jest najłatwiej. 'Odwalić' swoje i po sprawie.. W każdym razie, oby więcej było takich nauczycieli jak Ty Gustliku

pigor: ... dlatego, myślący nauczyciel (ka) − o ile jeszcze tacy(kie) są w szkołach − powinni olać − delikatnie mówiąc − debilną podstawę i uczyć jak im rozum, a nie jakiś urzędas w ministerstwie karze i tyle. ...

Baś: A ja odkąd poznałam Gustliku Twoją metodę wektorową liczenia pola trójkąta w analitycznej, to cały czas ją stosuję, cały czas zresztą napotykam na tego typu zadania. To świetnie, że dzielisz się swoją wiedzą Myślę, że nie tylko w swoim imieniu dziękuję.

Gustlik: Ja ten sposób uczenia matematyki opiszę bardziej obrazowo. Wyobraźmy sobie, że do Warszawy przyjeżdża osoba z innego województwa, aby tam zrobić sobie kurs prawa jazdy i zdać egzamin. Osoba ta nie zna Warszawy oraz tras prowadzących do podwarszawskich miejscowości. Pewnego dnia instruktor mówi do tego kursanta: jedziemy do Piaseczna, ale musimy jechać przez Wrocław, bo nie ma innej drogi. Kursant nie wie, gdzie jest Piaseczno i jaką drogą trzeba jechać, więc słucha potulnie instruktora. No i jadą obaj z Warszawy do Piaseczna przez Wrocław, jazda trwa kilkanaście godzin, zamiast np. 30 minut. Przychodzi czas egzaminu. Egzaminator każe kursantowi jechać z Warszawy do Piaseczna, nie wskazując oczywiście drogi. Kursant jedzie... przez Wrocław oczywiscie, bo tylko taką trasę zna. Efekt − wiadomo − egzamin oblany, bo kursant nie zdążył wykonać zadania. Nauczanie matematyki wygląda niemal identycznie jak ten kurs jazdy i potem matura niestety wygląda identycznie jak ten egzamin na prawko. Jest tylko jedna różnica: instruktora nauki jazdy można zmienić, jezeli jest kiepski, natomiast nauczyciela w szkole ciężko zmienić, a nawet jakby się to udało, to nowy na 99 % będzie pokazywał te same toporne sposoby nauczania.

Kasia: Brakuje tylko opcji 'lubię to' jak słowo daję!

Gustlik: Masz rację, Pigor. Dodam, że po wprowadzeniu nowej matury w 2010 roku i zarazem nowej spie...przonej podstawy programowej dzwoniłem do CKE, aby dowiedzieć się, czy nie ma jakichś wytycznych co do stosowanych metod i czy nie ma przymusu stosowania ich na maturze, bo chciałem się dowiedzieć, czy mogę uczyć uczniów krótszych metod. Rozmawiałem z matematykiem i ten powiedział mi, że uczeń ma prawo stosować każdą metodę, byleby tylko była poprawna i byleby nie popełnił błędów. Zapytałem też, czy uczeń może stosować metody nie objęte szkolną podstawą programową i czy może stosować wzory, których nie ma na karcie. Matematyk z CKE odpowiedział mi, że jak najbardziej, jako przykład podał stosowanie twierdzenia Menelaosa w zadaniach z geometrii. Tego twierdzenia nie ma nawet na rozszerzeniu, ale jeżeli uczeń je zna, to może jak najbardziej stosować. Niestety niektórzy nauczyciele wciskają uczniom kit, że nie można stosować innych metod, bo CKE nie zaliczy zadania, bo spotkałem się z tym kilka razy. Jest to NIEPRAWDA i każdy nauczyciel oraz uczeń powinien o tym wiedzieć. Nie wiem, co to ma na celu, czy jest to niewiedza nauczyciela czy chęć wywarcia presji na ucznia, żeby stosował tylko te metody,, co na lekcji i nie uczył się prostszych sposobów, podejrzewam, że chyba raczej to drugie.

kylo1303: Piszecie "ze nauczyciele powinni stosowac swoje metody i olac program". Problem w tym ze oni sa z tego rozliczani. O ile mozna rozszerzyc program to nie mozna go okroic. Chodzi mi tutaj o rozdzielenie dwoch spraw: bledow programowych i bledow nauczycieli. Dobrych nauczycieli z matematyki to ze swieca szukac. Sadze ze moj "profesor" nie jest zly, aczkolwiek tez wiele mozna mu zarzucic. Cos czego nie jestem w stanie pojac to to, ze nie nauczyl w klasie schematu Hornera. Stwierdzil ze lepiej stosowac dzielenie, bo gdy dzielimy przez wielomian wiekszego stopnia to horner nie pomoze. Takiego za przeproszeniem "debilizmu" nie rozumiem. Trafi sie na maturze zadanie z wielomianow, to zamiast 2min zajmie 10−15. Tym bardziej jak mamy szukac pierwiastkow nie−naturalnych... Trzecia sprawa (oprocz nauczycieli i programu) jest coraz nizszy poziom uczniow. Spoleczenstwo jest oglupiane co bardzo widac na przykladzie mlodziezy. Mldoziez jest glupsza− zmieniaja program− nauczyciele ucza mniej− uczniowie sa jeszcze glupsi. I kolo sie napedza. Mam nadzieje ze nie jest to chaotycznie napisane Popieram Cie Gustlik i az zobacze twoje komentarze w dzialach tematycznych.

Gustlik: 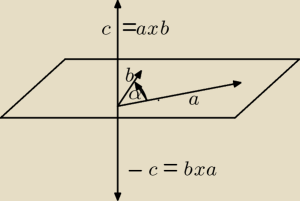Baś, cieszę sie, że podoba Ci się wektorowa metoda obliczania pola trójkąta, choc nie jest to moja metoda, a wzór wyprowadzony z iloczynu wektorowego. Ja kiedyś znalazłem ten wzór w tablicach i próbowałem dojść, skąd on się wziął. A wziął sie z "klasycznego" wzoru na pole trójkąta:

	1		1
P=		ah=		absinα, gdzie α to kąt między bokami a i b.
	2		2

Iloczyn wektorowy natomiast liczy się wzorem: c^→=a^→xb^→=|a^→|*|b^→|*sinα, gdzie |a→| i |b^→| to długosci wektorów, a α to kąt między nimi.

	1
Stąd wzór na pole trójkąta: P=		|a→xb→|
	2

W układzie współrzędnych iloczyn wektorowy można obliczyć wyznacznikiem: Jeżeli a^→=[a_x, a_y] i b^→=[b_x, b_y] to wyznacznik wektorów: d(a^→, b^→)= | a_x a_y | | b_x b_y | =a_x*b_y−a_y*b_x (na krzyż, podobnie jak w proporcjach)

	1		1
a pole trójkąta P=		|d(a→, b→}|=		|d(AB→, AC→)|.
	2		2

Na rysunku schemat obliczania iloc zynu wektorowego: reguła śruby prawoskrętnej − a^→xb^→ to kręcimy od a do b, czyli w lewo, śruba się wykręca do góry, stąd zwrot wektora c^→ do góry. Zmiana kolejności liczenia powoduje zmianę zwrotu wektora c^→, iloczyn wektorowy nie jest więc przemienny, otrzymujemy wektor przeciwny.

pigor: ..do kylo ja nie mówię olać program , ale olać podstawę programową, a to insza inszość , także nie mówię o stosowaniu swoich metod , tylko metod racjonalnych , itp, itd.

Basiek: Rozumiem, świetna sprawa, naprawdę bardzo przydatne. http://panmarek.sasiedzi.pl/ZESTAWIENIE/GEOMETRIA%20ANALITYCZNA/001-Rownanie%20prostej%20na%20plaszczyznie.htm Tu udało mi się znaleźć (na samym dole) 3 wzorki właśnie, ostatni to ten podany tu.

Gustlik: kylo1303, masz 100 % racji. Ja schemat Hornera pokazuję uczniom na podstawach, zresztą nawet tu na forum nie raz go pokazywałem, np. do rozwiązywania równań wielomianowych, dodam, że jest to jedna z moich ulubionych metod. Trafi się wielomian o trudnych do pogrupowania wyrazach, uczeń nie zauważy, że moze pogrupować np. wyraz 1 z 4 a 2 z 3 i leży. A jak zna schemat Hornera, tw. Bezout oraz twierdzenia o pierwiastkach całkowitych i wymiernych, to sobie poradzi w ten sposób. Pozdrawiam

kylo1303: Gustlik Mogłbys mi powiedziec gdzie moglbym przyblizyc sobie zastosowanie twierdzenia Monelaosa? Ewentualnie dac jakeis zadanko z tym zwiazane? Bo na wikipedii teorie przeczytalem, ale poki nie zrobie z tym zadania nie bede wiedzial jak efektywnie stosowac.

Gustlik: Dodam jeszcze, że wiele innych ciekawych metod z rozszerzeń lub nawet spoza nich przydalo mi się wiele razy do rozwiązywania zadań na poziomie podstawowym. Są to: − wyznacznikowa metoda rozwiązywania układów równań − uczę jej już od gimnazjum z bardzo dobrym skutkiem, − w geometrii analitycznej oprócz wspomnianego iloczynu wektorowego także iloczyn skalarny wektorów − służy m.in. do badania prostopadłości wektorów, − twierdzenie sinusów i cosinusów, − wzór Herona na pole trójkąta,

	y−B−yA
− wzór na współczynnik kierunkowy prostej przechodzącej przez 2 punkty a=
	xB−xA

oraz moje własne metody: − geometryczna metoda rysowania wykresów funkcji linioowej − tzw. metoda schodkowa: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41 , − metoda badania własności ciągów liczbowych za pomocą funkcji, − metoda "podjedź−cofnij" dla ciągów arytmetycznych i geometrycznych, polega na "startowaniu" z obliczeniami nie z wyrazu a₁, jak to się robi w szkole, tylko z wyrazu podanego w zadaniu i polega na dodaniu odpowiedniej liczby r−ów, gdy liczę wyrazy "do przodu" albo odjęciu r−ów przy liczeniu "do tyłu", np. a₈=a₅+3r, a₆=a₁₀−4r, dla ciągu geometrycznego licząc "do przodu" mnożę przez odpowiednią potęgę q, a "do tyłu" − dzielę, np.

	a9
a9=a4*q5, a7=		. Metoda ta wyeliminowała układy równań w większości zadan z
	q2

ciągami. − metoda x−ów w zadaniach geometrycznych ze stosunkami, np. stosunek 2:3 oznacza, że jeden bok ma długość 2x, a drugi 3x, zamiast układu równań mamy wtedy jedno równanie z x−em, − metoda "co masz dane, to obliczasz" w zadaniach geometrycznych, gdzie dane są takie wielkości, które zazwyczaj się liczy, jak obwód, pole, objętość, suma krawędzi. Oznaczam boki jako niewiadome, do tego stosuję zależności między bokami podane w zadaniu oraz ogólne wzory i liczę podaną wielkość, np. pole, za pomocą tych niewiadomych, a potem porównuję z wartościa pola podaną w zadaniu i otrzymanym równaniem wyliczam boki. Tę sama metodę stosuję w rachunku prawdopodobieństwa, gdzie dane jest prawdopodobieństwo, a nieznana jest np. liczba kul w urnie. − prosty sposób przekształcania równania okręgu: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1471 . I wiele innych ciekawych sposobów.

Gustlik: kylo1303 Szczerze mówiąc nie spotkałem się jeszcze z zadaniem wymagającym stosowania tego twierdzenia, ale jak tylko znajdę coś takiego, to zamieszcze na forum. Pewnie dlatego, że nie ma go w szkole i nie było go nawet 24 lata temu, gdy zdawalem maturę, a program był wtedy naprawdę wyśrubowany. Ale wiem, jak należałoby je stosować. Ja tylko zacytowałem słowa matematyka z CKE.

kylo1303: To tak moze wypunktuje twoje metody, oceniajac je pod katem stosowania przez moja wlasna osobe i postaram sie ocenic ich przydatnosc, zaczne od konca: 1. okregi− znajomosc tych "wzorkow" bardzo pomaga, ale zawsze jest to dodatkowa rzecz do zapamietania. W tablicach tego nie ma wiec maturzysta musi albo zapamietac i byc ich pewny, albo o nich zapomniec.Sęk w tym ze wystarczy pomylic "−" we wzorze i juz zadanie leci. Najlepiej jest, gdy uczen "rozumie" wzor, a jeszcze lepiej jak potrafi go wyprowadzic. Dlatego tez osobiscie przy zamianie postaci robie cos w tym guscie: x²+y²−4x+6y−20=0 Automatycznie nastepuje zamiana: (x−2)²+(y+3)² .....= 0 W miejsce kropek przepisuje wyraz wolny z pierwszego rownania, a potem odejmuje kwadratu z nawiasow: ... −20−4−9=0 Innymi slowy znam obie metody ale jednak wole "nie skracac" wzorami bo wg. mnie latwiej sie pomylic. A czasu nie zabiera wiecej. − metoda "co masz dane, to obliczasz" − prawde powiedziawszy czasami jesli tego nie zastosujesz to nie da sie zrobic zadania − metoda x−ów, stosuje od zawsze, i wydaje mi sie ze jest tez uczona w szkolach. −metoda "podejdz/cofnij" −tego nie stosuje. Zazwyczaj uzalezniam wszystko od a₁ i r czy tam a₁ i q. I czasami nacialem sie na tym, bo przyjmujac dane: a,a+r,a+2r nie dalo sie zrobic zadania, natomiast przy zapicie a−r,1,a+r juz tak. Takze jak najbardziej plus dla twojej motedy. −metoda schodkowa− stosuje, jak ktos mysli logicznie to korzysta nawet jak nikt go nie nauczyl − metoda badania własności ciągów liczbowych za pomocą funkcji,− nie znam − co do wektorow to mam spore zaleglsoci, wzor na pole trojkata metoda wyznacznikowa znam i stosuje, ale tak to musze nadrobic ten dzial. Wiem ze to co pisze nijak moze polemizowac z tym co ty napisales (+ nie wnosi za bardzo nic nowego), w koncu roznica doswiadczenia jest ogroma. Uwazam tylko ze czasem mozna cos zauwazyc i poprawic. Twoje sposoby sa skuteczne i biora sie po prostu z logicznego (zeby nie powiedziec "normalnego") myslenia. A z tym coraz gorzej, nawet u niektorych nauczycieli.

Alkain: Basiek ! Dziękuję ze ten link w twoim poście, fajna sprawa z tym trójkątem

Gustlik: kylo1303, co do równania okręgu uważam, że ktoś wreszcie powinien wyprowadzić i zastosować te wzory oraz podać je w tablicach, bo uczniowie metodą wzorów skróconego mnożenia się męczą. Wolą moją metodę, niż kombinacyjną, bo trzeba wymyśleć i sztucznie dodać liczbę, a potrem ja odjąc, a nie każdy widzi, jak to robić, nie każdy widzi, skąd to −20−4−9. Metoda na wzory skróconego mnożenia wg mnie toporna i najgorsza z możliwych. Metodę badania własności ciągów liczbowych za pomocą funkcji wykorzystuję przede wszystkim do badania monotoniczności ciągów. Stosuję ją zamiast metody "a−_n+1−a_n, gdy ciąg jest dany wzorem łatwej do zbadania funkcji, np. liniowej, kwadratowej, homograficznej czy wykładniczej. Polega ona na tym, że we wzorze ciągu zamieniam "n" na "x", a "a_n" na "y" i w ten sposób robię funkcję z ciągu. Następnie badam monotoniczność tej funkcji w standardowy dla danej funkcji sposób, np. rysując wykres, po czym badam, jak zachowuje się ta funkcja dla liczb dodatnich, albo odczytuję ze wspólczynników występujących we wzorze. Np. gdy ciag jest dany wzorem funkcji liniowej (wtedy jest to ciag arytmetyczny), to odczytuję monotoniczność ze współczynnika kierunkowego prostej (jest on równy różnicy tego ciągu). Np. a_n=3n+4 jest rosnący, bo a=3>0, a_n=−4n+2 jest malejący, bo a=−4<0, a_n=3 jest stały, bo a=0. Ze współczynników widać też, jak zachowuje się ciąg "wykładniczy" (czyli geometryczny) oraz w większości przypadków "homograficzny", choć w przypadku hiperboli trzeba nieraz narysowac wykres, bo bywa, że asymptota pionowa jest na dodatniej półosi OX. Metoda "na funkcję" nieraz wymaga narysowania wykresu, chociaż przybliżonego. Tak jest, gdy ciąg jet dany np. wzorem funkcji kwadratowej, np. a_n=n²+5n+6. Badam, gdzie jest wierzchołek paraboli, liczę p i rysuję przyblizony wykres funkcji zaznaczając p na osi OX i skierowując ramiona paraboli we właściwą stronę. Wtedy widać jak na dłoni, czy ciąg jest rosnący, czy malejący albo niemonotoniczny. Tę samą metodę "na wykres" stosuję do ciągów z wartością bezwzględną, np. a_n=|n−6|. Rysuję wykres funkcji y=|x−6| i wszystko widzę. Jest mniej pracy i łatwiej, niż liczeniem. Niemniej jednak metodę obliczeniowa a_n+1−a_n też pokazuję, bo w przypadku trudniejszych ciągów bywa ona łatwiejsza. Pozdrawiam

kylo1303: Dziekuje za bardzo przejrzyste przedstawienie tego sposobu. Bardzo przydatne, chociaz na maturze chyba musialbym dolaczyc jakis komentarz (skad z ciagu zrobila sie funkcja). Co do watku z okregiem, raczej moja mocna strona sa rachunki w glowie, natomiast nie lubie zapamietywac wzorow. Bo czesto potem nie jestem ich pewien i i tak musze je sobie wyprowadzic Ale dla wiekszosci uczniow zapamietanie 3 prostych wzorow byloby latwiejsze od stosowania metody grupowania wyrazow i skroconego mnozenia.

Mateusz: Ciąg liczbowy to jest funkcja tyle ze dziedziną tej funkcji jest tylko i wyłącznie zbiór N⁺ po prostu

Gustlik: Jeszcze jedna sprawa: trygonometria − schemat strzałkowy do obliczania funkcji w trójkącie prostokątnym: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=397 oraz jego zastosowanie do funkcji dowolnego kąta: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=417 oraz: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=453 , https://matematykaszkolna.pl/forum/forum.py?komentarzdo=455 , https://matematykaszkolna.pl/forum/forum.py?komentarzdo=457 , https://matematykaszkolna.pl/forum/forum.py?komentarzdo=458 .

kylo1303: Mysle ze strzelki bylyby pomocne na poczatku, w pozniejszym toku edukacji robi sie to odruchowo. Ale Gustlik naprawde masz sporo fajnych pomyslow. Pozazdroscic twoim uczniom

Mila: Gustlik nie cierp za miliony! To było dobre w epoce romantyzmu. Co ma być to będzie.

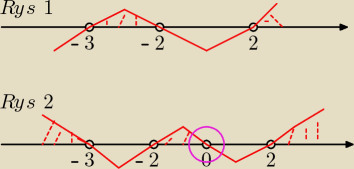
Gustlik: Ja nie cierpię za miliony. Tylko szlag mnie za przeproszeniem trafia na te durnowate niektóre metody, które robią mętlik uczniom w głowie. Dzisiaj robiłem zadanie z rozszerzonej matury − trzeba było rozwiązać nierówność wielomianową 3 stopnia. I wiecie co? Chłopak rozłożył poprawnie wielomian na czynniki, wyszły 3 pierwiastki i na oś naniosł te liczby oraz 0. Ja się pytam, czemu on nanosi 0 na oś, skoro nie było ono pierwiastkiem tego wielomianu, odpowiedział mi, że pani w szkole tak uczy. Ja od wielu lat walczę z tym zaznaczaniem zera na osi w nierównościach już od gimnazjum oczywiście w sytuacjach, gdy nie jest ono rozwiązaniem (pierwiastkiem) danej nierówności, bo potem uczeń nabiera takiego nawyku i przy nierównościach wyzszych stopni podczas rysowania wykresu traktuje zero jak pierwiastek i rysuje przez nie wykres i mamy poważny błąd. Np. nierówność (x+3)(x−2)(x+2)>0 rozwiązujemy tak: x=−3, x=2, x=−2 rysujemy wykres jak na rys. 1 i mamy przedział x∊(−3, −2)U(2, +∞). Na rys. 2 przedstawiłem typowy błąd rysowania wykresu spowodowany naniesieniem zera na oś przez ucznia, "bo pani tak uczy". Zero brane jest przez wielu uczniów za rozwiązanie i całe zadanie do bani, bo wykres spiep...rzony. Należy pamięrać: ZERO NANOSIMY NA OŚ TYLKO WTEDY, GDY JEST ONO PIERWIASTKIEM WIELOMIANU !

Gustlik: 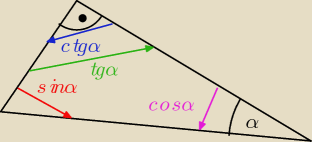Kylo1303 dzięki tym strzałkom oraz wierszykowi: Sinus − w opozycji Cosinus − w koalicji Tangens − do domu Cotangens − z domu nauczyłem wielu uczniów rozwiązywania zadań z funkcjami trygonometrycznymi bez obracania kartki, gdy trójkąt był narysowany "krzywo" albo "do góry nogami" , jak np. na rysunku. Wierszyk mówi, gdzie trzeba rysować strzałkę danej funkcji. Uczniowie wcześniej obracali kartkę tak, aby "postawić" trójkąt na którejś z przyprostokątnych, a ja ich nauczyłem robić bez obracania. Tylko wystarczyło zapamiętać, gdzie która strzałka ma lecieć. Pomógł właśnie ten wierszyk. Poza tym pomagają one przy obliczaniu pozostałych funkcji tryg., gdy dana jest jedna z nich, nie trzeba robić tego wzorami, wystarczą strzałki i twierdzenie Pitagorasa, o wiele szybciej. Pozdrawiam

Jolanta: A biedny uczen tylko moze włosy z głowy wyrywac z rozpaczy.Też myślałam,ze nie wolno korzystac z wzorów,których nie ma na podstawie.

b.: może jestem ciemny, ale kompletnie nie rozumiem, jak np. wers 'Sinus − w opozycji' miałby mi pomóc w narysowaniu właściwej strzałki −− w opozycji są, jak dla mnie, również strzałki zielona i niebieska, a także strzałka przeciwna do czerwonej. Mam też wrażenie, że nauczenie sie tego wierszyka oraz jego właściwej interpretacji, a następnie rysowanie strzałek wg niego zajęłoby mi więcej czasu niż nauczenie się na pamięć co się dzieli przez co. W końcu to jest jedna z takich rzeczy, których sie po prostu trzeba nauczyć na pamięć i nie jest to znowu jakies nie wiadomo co, tego się człowiek uczy automatycznie po zrobieniu pewnej liczby zadań, które i tak trzeba zrobić, żeby sie jakoś orientować.

pigor: b zgadzam się z tobą , i to co pan G wymyśla nie powinno kręcić (podniecać) uczniów , bo wierszyki , strzałki itp. bzdety, dobre są dla ... prawej półkuli np. na polskim , ale nie na matematyce (... , a co z lewą półkulą ) ... i tyle

asdf: Nie bardzo widzę nauczenia się tych strzałek. Na początku może pomóc, a później to już to się robi z automatu jak zrobi się trochę zadań. To jak z nauką jazdy, na początku instruktor podpowie, że przy zmianie biegów wciska się sprzęgło, ale to trzeba sobie wpoić jeżeli chce się samemu jeździć. Tak samo z funkcjami trygonometrycznymi, trzeba to sobie wpoić, żeby samemu robić zadania.

krystek: @Gustlik wytłumacz uczniowi ,że Δ prostokątny ma dwie przyprostokątne ,aby je odróżnić (tak jak z nazwiskami takimi samymi −mamy imię) mówimy przyprostokątna przy danym kącie i przyprostokątna leżąca na przeciw danego kąta. I definicji uczeń musi się nauczyć. Twoje" opzycje " "kalcje "... to uczenie bez zrozumienia. A dla dowolnego kąta posługujemy się x, y i r i wówczas uczniowie nie maja kłopotów z wzorami redukcyjnymi, znakami funkcji w poszczególnych ćwiartkach itd itp. Kiedy zaprzestaniesz narzucania "jedynej słusznej metody"?

kylo1303: asdf Mam takie samo zdanie. pigor Nic bardziej blednego. Najlepiej jest laczyc obie polkule. Ogolnie wizualizacje, wierszyki, skojarzenia to bardzo dobre narzedzia do zapamietywania. Profesjonalisci moga ci ulozyc historyjke nawet do bardzo skompikowanego wzoru, dzieki czemu latwiej zapamietac. Gustlik A co do rozwiazywania nierownosci wielomianowych to masz racje. Najlepsza i najszybsza metoda jest oczywiscie zaznaczyc miejsca zerowe, sprawdzic szybko jeden skrajny argument i zastosowac "wężyka". Nie rozumiem dlaczego wiele osob korzysta z siatki znakow czy innych sposobow− dlugo i malo wydajnie. A zaznaczenie 0 na osi kazdego mogloby zmylic, dodatkowy czynnik przez ktory mozna zwalić zadanie.

Gustlik: Krystek, Pigor, b Oczywiście macie sporo racji. Ja też pokazuję standardowe definicje, twierdzenia i wzory, ale w zadaniu rzeczą najważnmiejszą jest umiejętność zastosowania danego wzoru, niż zapamiętanie regułki, często niezrozumiałej dla ucznia. Co do funkcji trygonomwtrycznych cztery definicje w stylu "stosunek przyprostokątnej przeciwległej do przeciwprostokątnej" są takim samym łamańcem, jak "W Szczebrzeszynie chrząszcz brzmi w trzcinie" albo "Stół z powyłamywanymi nogami", zwłaszcza, ze nazwy boków trójkąta brzmią podobnie i łatwo się pomylić. Natomiast wierszyk łatwo wpada w ucho i uczeń jak skojarzy "sinus w opozycji" po kilku zadaniach prawidłowo rysuje strzałkę i prawidłowo oblicza daną funkcję. Dla niego to sformułowanie jest łatwiejsze do zapamiętania, niż standardowa regułka z podręcznika, a chyba najważniejsze są prawidłowe obliczenia, bo na maturze nikt nie pyta o regułki, tylko dostaje się zadania do liczenia. Proponuję poczytać coś na temat mnemotechniki − czyli sposobów ułatwiających zapamiętanie pewnych informacji, wzorów czy regułek, np. tutaj: http://pl.wikipedia.org/wiki/Mnemotechnika . Co do wzoerów redukcyjnych − dwie proste regułki: 1. Reguła kofunkcji − dla katów (90^o+−α), (270^o+−α) i ich odpowiedników w radianach, czyli zaczynających się od nieparzystej krotności kata prostego funkcje zmieniają nazwy, np. sin na cos, cos na sin, tg na ctg, a ctg na tg. Dla kątów (180^o+−α), (360⁺−α) czyli od parzystej krotności kąta prostego nazwy funkcji pozostają bez zmian. 2. Prosty wierszyk o znakach funkcji trygonometrycznych: W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus. Te dwie zasady umożliwiają szybkie wyprowadzenie wzoru redukcyjnego, który nam w danym momencie jest potrzebny.

Gustlik: Do Jolanty i nie tylko. Uczeń ma prawo korzystać z każdego wzoru i metody, również takiej, której nie ma w podstawie programowej dla szkół średnich nawet na poziomie rozszerzonym, ważne tylko, żeby to była metoda prawidłowa no i oczywiście żeby nie popełnił błędów. Na szczęście CKE nie narzuca metod, te toporne metody w stylu "z Warszawy do Wrocławia przez Pekin" to chory wymysł wielu nauczycieli (nie wszystkich na szczęście), często niedouczonych i nie znających innych metod, co Jakub nazywa słusznie intelektualnym lenistwem. Pal licho, jeżeli nauczyciel uzna inną metodę, połapie się, o co w niej chodzi i uzna zadanie rozwiązane przez ucznia na sprawdzianie, takiego nauczyciela można jedynie pochwalić, ale są tacy, którzy komentują to tak: "Ja tak nie uczyłem/am", "Masz to robić tylko tym sposobem, bo CKE innego nie uzna" (nic bardziej mylnego), albo "Ciąg to nie funkcja" jak skomentowała to jedna z nauczycielek z LO w moim mieście i zabierają punkty za tak rozwiązane zadanie, mimo prawidłowej metody. Chodziło o sposób badania monotoniczności ciągów za pomocą funkcji, opisany zresztą powyżej. Hasło to do dzisiaj jest znane w tej szkole jako "twierdzenie M." i wszyscy uczniowie za przeproszeniem łacha drą z tej nauczycielki.

Gustlik: Kylo1303, ja stosuję tę samą zasadę rysowania wykresów wielomianów, co Jakub, tylko dla ułatwienia zapamiętania nazwałem ją "zasadą prawego ramienia". Otóż dla wszystkich wielomianów prawe ramię wykresu zachowuje się identycznie − leci w górę, gdy współczynnik pierwszego wyrazu wielomianu − tego przy najwyższej potędze x (dla ułatwienia nazywam go współczynnikiem "kierunkowym" w cudzysłowiu) jest dodatni, oraz w dół, gdy ten współczynnik "kierunkowy" jest ujemny. Pokazuję przy tym analogię do funkcji liniowej (prosta) i kwadratowej (parabola). To prawe ramię po prostu zachowuje się tak samo jak ramiona paraboli, co uczniowi jest łatwiej zapamiętać, dlatego uczę, żeby wykres rysować od prawej strony, a nie od lewej. Druga sprawa to krotności pierwiastków − krotność parzysta − wykres "odbija się" od osi OX, krotność nieparzysta − przecina oś. Jeszcze jedna ważna sprawa − dla wielomianów nieparzystego stopnia oba ramiona wykresu są skierowane w przeciwne strony − jedno ramię w górę, a drugie w dół, jest to analogia do funkcji liniowej, a dla wielomianów stopnia parzystego oba ramiona są skierowane w tę samą stronę (albo oba w górę, albo oba w dół, jak w paraboli. To umożliwia uczniowi sprawdzenie, czy prawidlowo narysował wykres. Wyjaśniłem tę zasadę tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=142 .

Gustlik: Tak samo wkurza mnie szkolna metoda przesuwania wykresów funkcji, którą ja nazwałem metodą "Jak dojśc na pocztę". Te określenia 2 jednostki w prawo, 4 w dół kojarzą mi się z tym, jak idę nieraz ulicą, zatrzymuje mnie jakiś przechodzień albo kierowca będący spoza mojego miasta i pyta np. "jak dojść na poczte". Ja mu wtedy tłumaczę: musi pan/i skręcić w lewo, potem w dół i będzie pan/i na poczcie. Owszem można uczniowi to tak wytłumaczyć, ale język matematyki to język wektorów. Jak to tłumaczę tak: po przesunięciu mamy wzór funkcji y=f(x−p)+q i otrzymujemy go przez przesunięcie wykresu funkcji y=f(x) o wektor w^→=[p, q]. Oczywiście najpierw pokazuję, co9 to jest wektor i jak sie oblicza jego współrzędne. Tłumaczę też, że podczas odczytywania ze wzorów funkcji p zmienia znak, a q nie zmienia znaku, np. dla funkcji y=f(x+3)−4 p=−3, q=−4, wykres przesunie się o wektor [−3, −4] czyli o 3 w lewo i o 4 w dół. Celowo też wprowadziłem oznaczenia tych współrzędnych − p i q − wziąlem je z postaci kanonicznej funkcji kwadratowej, a nie jak niektórzy to robią a i b, tymi literami często oznacza się inne współczynniki występujące we wzorach funkcji, np. w funkcji liniowej y=ax+b a to współczynnik kierunkowy, a b to wyraz wolny, w funkcji wykładniczej y=a^x a to podstawa potęgi itp. A tak wiadomo − p i q, bo te współrzedne we wszystkich rodzajach funkcji "działają" tak samo, w ten sam sposób przesuwają wykres, nie widzę więc potrzeby oznaczania ich inaczej przy funkcji kwadratowej a inaczej przy innych funkcjach. Uczeń wtedy szybko zapamięta, jak się odczytuje p a jak q i potem prawidłowo przesuwa każdy wykres, jak ma ujednoliconą metodę do wszystkich rodzajów funkcji. Łatwo też zapamiętuje potem postać kanoniczna funkcji kwadratowej, zresztą ja właśnie tłumaczę zasadę przesuwania wykresów głównie na paraboli, bo ten wykres świetnie się nadaje na wzorzec ze względu na to, że p i q to współrzędne wierzchołka paraboli i widać, jak działa to przesuwanie.