. Kasia: Proszę o pomoc. Bardzo proszę o pomoc z dwoma zadankami, z którymi niestety nie mogę sobie poradzic. Ta cała stereometria to niestety czarna magia dla mnie, o ile z prostymi dla mnie zadaniami moge sobie poradzic, to juz z ciut trudniejszymi jest koszmar.. Z góry dziękuję za jakąkolwiek pomoc! 1. Podstwą ostrosłupa jest równoległobok o bokach długosci 6cm, 10 cm i kącie ostrym 30 stopni. Spodkiem wysokosci ostroslupa jest punkt przeciecia przekatnych podstawy. Kat dwuscienny, wyznaczony przez mniejsza sciane boczna i plaszczyzne podstawy, ma 60 stopni. Oblicz: a) wysokosc ostroslupa b) tanges kata nachylenia wiekszej sciany bocznej do plaszczyzny podstawy ostroslupa 2. W ostroslupie prawidlowym czworokatnym wszystkie krawedzie maja taka sama dlugosc a. a) oblicz objetosc tego ostroslupa w zaleznosci od dlugosci a. c) w jakiej odleglosci od wierzcholka ostroslupa nalezy poprowadzic plaszczyzne rownolegla do podstawy, aby pole otrzymanego przekroju bylo dwa razy mniejsze od pola podstawy?

Kasia: odświeżam.

Kasia: ponawiam bardzo liczę na jakąś pomoc..

Skipper:

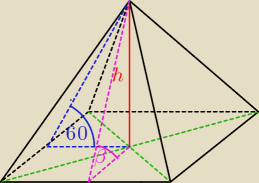
h
	=tg60o
5

h=5tg60^o=5√3

h
	=tgβ ... β=?
3

Skipper:

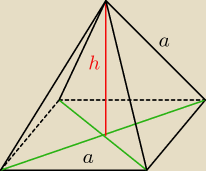
	a√2
h2=a2−(		)2
	2

	a2		a√2
h2=		... h=
	2		2

	1
V=		ah ... itd ...
	3

asdf:

	a√2
H = a −
	2

	1		√2
V =		a2 * a(1 −		)
	3		2

dobrze?

Kasia: 1. zadanko w calosci rozumiem a co do 2. mam pytanie, czyli pozniej do wzoru na objetosc w

	a√2
miejsce h podstawiam to co wczesniej sie wyliczylo wyliczylo czyli		tak? a
	2

moglbys/as mi pomoc jeszcze z tym kolejnym podpunktem? bo wydaje mi sie bardzo zagmatwany i dziekuje juz bardzo za pomoc i piękne rysunki, zazdroszcze takiej cierpliwosci i zdolnosci do widzenia przestrzennego..

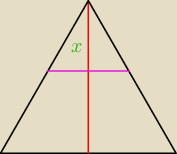Skipper: cd ...

	a2		a
aby pole przekroju było równe		... bok przekroju ma być równy
	2		√2

x		h
	=		... x=?
a   √2		a

asdf: @Skipper Ile Ci wyszło w 2a)?

Kasia:

	a
dlaczego bok przekroju musi byc rowny		? z czego to wynika?
	√2

Skipper: ... tam powinno być

	1		√2
V=U{1}{3]a2h .... czyli		a3
	3		2

Skipper:

	a		a2
... bo (		)2=
	√2		2

Kasia: okej jasne a pozniej ten stosunek wzial sie z tw. Talesa? i mam 2 niewiadome x i a, tak? i mam po prostu wyznaczyc x nic nie robiac z tym a, tylko po prostu przeksztalcajac? oczywiscie po uprzednim podstawieniu h tym co wczesniej wyznaczyles.

Skipper: jasne−

Kasia: rozumiem dziękuję Ci ogromnie za pomoc bardzo mi pomogłeś