geometria koko: w trapezie ABCD o podstawach AB i CD wiadomo ze |AB|=3|CD|. Punkt S jest punktem przeciecia sie przekatnych trapezu. Wyznacz pole trapezu jesli pole trojkata BCS = 1/3

Eta:

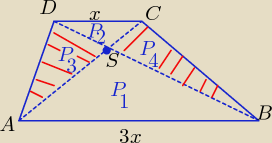
	3x
Δ ABS ~ ΔDCS w skali k=		= 3
	x

	P1
to:		= k2=9 ⇒ P1= k2*P2=9*P2
	P2

	1
PΔADS= PΔBCS =
	3

	1		1
P3=P4= k*P2 ⇒ 3P2=		⇒ P2=
	3		9

P(tr)= P₁++2*P₃+P₂ = k²*P₂+2*k*P₂+P₂= P₂(k²+2k+1)

	1		16
P(tr)= (k+1)2*P2= 42*		=
	9		9

koko: swietne rozwiazanie, dzieki za pomoc!

nick: sorry a skąd się wzięło P4= k*P2?

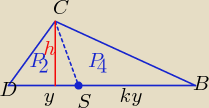Eta: Trójkąty DCS i BCS mają wspólną wysokość i proporcjonalne podstawy y i ky

	y*h
PΔDCS= P2=
	2

	ky*h
PΔBSC=P4=		= k*P2
	2