dowód
Kia: W czworokącie ABCD dwusieczne dwóch kolejnych kątów wewnętrznych o wierzchołkach A oraz B
przecinają się w punkcie K. Przez punkt K poprowadzono odcinek równoległy do boku AB i
przecinający boki AD i BC odpowiednio w punktach L i M. Uzasadnij, że |AL| + |BM| = |LM|.
9 kwi 18:59
Basia:
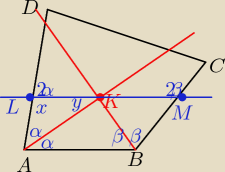
x = 180−2α
y = 180 − α − x = 180 − α − 180 + 2α = α
stąd wynika, że AL=KL
analogicznie wykaż, że BM = KM
i koniec
9 kwi 19:08
rumpek:
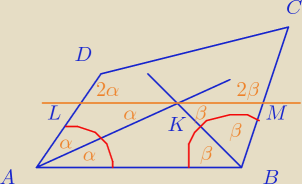
Teza: |AL| + |BM| = |LM|
Trójkąty △AKL i △KBM są równoramienne, dalej wystarczy tylko podobieństwem trójkątów

9 kwi 19:10
rumpek:
Tak
Basi sposób jest zdecydowanie łatwiejszy

Wystarczy sprowadzić oznaczenia:
|AL| = |LK| = x
|BM| = |MK| = y
|LM| = x + y
|AL| + |BM| = x + y
x + y = x + y
|LM| = |AL| + |BM|
c.n.u.


9 kwi 19:13
Kia: dzięki wielkie

9 kwi 19:23
 x = 180−2α
y = 180 − α − x = 180 − α − 180 + 2α = α
stąd wynika, że AL=KL
analogicznie wykaż, że BM = KM
i koniec
x = 180−2α
y = 180 − α − x = 180 − α − 180 + 2α = α
stąd wynika, że AL=KL
analogicznie wykaż, że BM = KM
i koniec
 Teza: |AL| + |BM| = |LM|
Trójkąty △AKL i △KBM są równoramienne, dalej wystarczy tylko podobieństwem trójkątów
Teza: |AL| + |BM| = |LM|
Trójkąty △AKL i △KBM są równoramienne, dalej wystarczy tylko podobieństwem trójkątów 
 Wystarczy sprowadzić oznaczenia:
|AL| = |LK| = x
|BM| = |MK| = y
|LM| = x + y
|AL| + |BM| = x + y
x + y = x + y
|LM| = |AL| + |BM|
c.n.u.
Wystarczy sprowadzić oznaczenia:
|AL| = |LK| = x
|BM| = |MK| = y
|LM| = x + y
|AL| + |BM| = x + y
x + y = x + y
|LM| = |AL| + |BM|
c.n.u. 

