niech k, l, m, n beda srodkami krawedzi malinka: Niech K, L, M, N będą środkami krawędzi czworościanu foremnego ABCS. Udowodnij, że przekrój KLMN tego czworościanu jest kwadratem. Proszę o pomoc, nie mam pojęcia jak się za to zabrać. Z góry dzięki

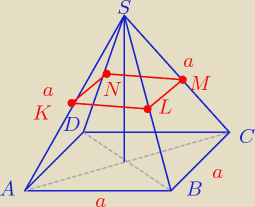
rumpek: Zauważmy, że skoro mamy podaną informacje, że jest to czworościan foremny, ponadto punktu odpowiednio K, L, M, N są środkami krawędzi bocznych to:

	a
* odcinki |KL| oraz |MN| mają długość		(ponieważ, są środkami)
	2

	a
* odcinki podobnie jak wyżej |KN| oraz |ML| mają długość		(tak jak wyżej)
	2

Zatem wszystkie odcinki są równe, zatem jest to kwadrat c.n.u.

rumpek: W zasadzie to jeszcze nie koniec, udowodnienie że ma równe boki nie świadczy o tym, że jest o kwadrat (romb też ma boki takiej samej miary). Trzeb dodać, że odcinki |KL| i |MN| są równoległe do podstawy , (można dowieść tego na podstawie podobieństwa trójkątów [Talesa]). Z bokami |KN| i |LM| podobnie − równoległe do podstawy . Widać, że jest to dokładnie kwadrat

	1
w skali		do kwadratu podstawy
	2

malinka: Twój dowód nie dotyczył czworościanu foremnego :X. Czworościan foremny ma w podstawie trójkat....

rumpek: ups ale co się przejmujesz dowód, będzie ten sam, tylko rysunek zmień

rumpek: Tak dowód dokładnie taki sam, tylko zmienisz oznaczenia, wystarczy pomyśleć

malinka: ok, super zaraz wszystko prześledzę

Buuu: Prawidłowy rysunek do zadania.