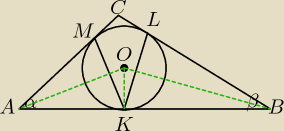
kąty zbk : W trójkąt ABC w którym miara kąta BAC wynosi α, a miara kąta ABC wynosi β, wpisano okrąg. Punkty K, L, M są punktami styczności okręgu odpowiednio z bokami AB, BC i AC. Wykaż, że kąt

	α+β
MKL=
	2

moje wnioski połącze AO i mam dwusieczną kąta MAK tak samo z drugiej strony oraz połącze OK powstają dwa trójkąty prostokątne i dalej mam kłopot wiadomo kąt AOK będzie 90−α kąt KOB tak samo i dalej mam kłopot prosze o pomoc

rumpek:

	α + β
Teza: |∡MKL| =
	2

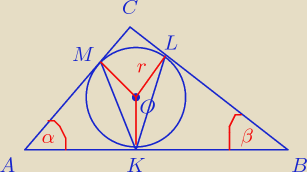
Dowód: |∡ACB| = 180^o − α − β. Rozpatrzmy czworokąt MOLC ma on dwa kąty proste (promienie się stykają) Bez trudu obliczymy kąt: |∡MOL| = 360^o − 90^o − 90^o − 180^o + α + β = α + β

	α + β
Teraz z wiadomości o kącie środkowym wiemy, że |∡MKL| =
	2

c.n.u. [https://matematykaszkolna.pl/strona/465.html ]

Basia: KOM = 360−90−90−α = 180−α KOL = 360−90−90−β = 180−β MOL+KOM+KOL = 360 MOL = 360 − 180+α − 180 + β = α+β

	MOL		α+β
MKL =		=
	2		2

zbk : dzieki wielkie

pigor: np. tak :z warunków zadania : |∡ACB|=|∡MCL|=180^o−(α+β) , a łącząc O z M i O z L otrzymuję środkowy ∡MOL oparty na łuku (cięciwie) ML ; dalej OM ⊥ AC i OL ⊥ BC, czyli |∡OMC|+|∡OLC|=180^o w czworokącie MCLO, to |∡MOL|+|∡MCL|=180^o ⇔ |∡MOL|=180^o−MCL|=180^o−[180^o−(α+β)]= 180^o−180^o+(α+β)=α+β , zatem |∡MKL| = ¹₂|∡MOL|= ¹₂(α+β) c.b.d.w. − jako kąt wpisany w kolo oparty na tym samym łuku co środkowy ∡MOL . ...