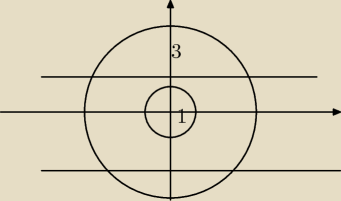
Czy mógłby ktoś to sprawdzić???? karla: Czy mógłby ktoś to sprawdzić 1.Dany jest układ równań y = x + p ( x2 + y2)2 – 10( x2 + y2) + 9 = 0 Podać interpretację geometryczną tego układu i na tej podstawie określić wartość parametru p tak, aby układ ten miał dokładnie dwa rozwiązania. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− rysunek x² + y²=1 x² + y²=3 ⇒⇒⇒p=(1;3)v(−3;−1) proszę o sprawdzenie

Jack: Wstaw pierwsze równanie do drugiego i wyznacz współczynnik p dla Δ>0. Wtedy otrzymasz dwa punkty przecięcia prostej z okręgiem, czyli dwa rozwiązania. To co napisałeś... nie jest ok

karla: achaaaaaaa

Jack: zakładam, że drugie równanie opisuje okrąg (zasugerowałem się rysunkiem)! Na pewno układ jest dobrze przepisany?

karla: tak

karla: Ale to po przemnożeniu wyjdzie coś dziwnego nie może być tak jak ja mam?

karla: nie może być tak jak ja mam?

karla: czy może mi to ktoś wytłumaczyć

Basia: t=x²+y² czyli t∊<0;+∞) t²−10t+9=0 Δ 100 − 36 = 64 t₁ = ¹⁰⁻⁸₂ = 1 t₂ = ¹⁰⁺⁸₂ = 3 i masz x²+y²=1 O(0,0) r₁ = 1 x²+y²=3 O(0,0) r₂ = √3 y = x+p to proste równoległe do prostej y=x dokładnie dwa punkty wspólne ta prosta z sumą okręgów będzie miała gdy będzie leżała między styczną do małego okręgu i styczną do dużego czyli 1. szukamy stycznej do małego okregu układ równań ma mieć jedno rozwiązanie y = x+p x²+y²=1 znajdujemy p₁ i p₂ dla którego Δ=0 2. szukamy stycznej do dużego okręgu układ równań ma mieć jedno rozwiązanie y = x+p x²+y²=3 znajdujemy p₃ i p₄ dla którego Δ=0 p∊(p4; p₂)∪(p₁; p₃)