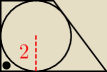
trapez Ergo: Witam, ZAD: Trapez prostokątny opisany na okręgu o r=2 ma jedną podstawę dwa razy dłuższą od drugiej. Oblicz obwód tego trapezu. Proszę o jak najszybszą pomoc.

asdf:

Maciek: górna podstawa a, dolna 2a

Maciek: wysokość 4 i ramię trapezu r

Maciek: skoro czworokąt jest opisany to zachodzi równość a+2a=4+r

Ergo: Ale jak obliczyć a i ramię

Maciek: a r da się wyliczyć z Δ prostokątnego 4²+a²=r²

Maciek: czyli r=√16+a²

Maciek: czyli 3a−4=√16+a²

Maciek: podnieś obie strony do kw.

Maciek: (3a−4)² = 16+a²

Maciek: czyli po redukcji 8a²−24a=0

Maciek: 8a(a−3)=0

Maciek: a=0 lub a=3 oczywiście zerem długość boku nie może być (a>0)

Maciek: czyli Obw. możemy już łatwo policzyć

Maciek: Obw = 4+3+3+3+5 = 18

Maciek: Miłego świętowania

Ergo: Wielkie dzięki. Udało się. Mam jednak jeszcze jedno zadania:

	1
ZAD. Dane sa parabole: f(x) =		x2 + 2x + 4 i g(x) = −x2 + 4x − 3.
	2

Niech d(x) oznacza odległość między punktami P₁(x,f(x)) i P₂(x,g(x)), o tej samej pierwszej współrzędnej x, należącymi odpowiednio do pierwszej i drugiej paraboli. a) Wyznacz wartość x, dla której d(x) = 7 b) Jaka jest najmniejsza wartość d(x) Wogóle nie wiem jak to zrobić. Czapki z głów dla tego kto to dobrze rozwiąże. Jest dosyć trudne jak na poziom maturalny. Z chęcią poznam jak to zrobić. Pomóżcie

Baś: Jestem leniwcem z natury, więc tylko tak pobieżnie na pierwszy rzut oka: jedna z parabol musi leżeć nad drugą, mają przeciwnie skierowane ramiona, może też się przecinają. Punkty P₁ i P₂ mają te samą współrzędną x, a współrzędną y wyznaczają jakby...

	1
wzory paraboelek. Więc odległość d(x)=|y1−y2|= |		x2 + 2x + 4− (−x2 + 4x − 3)|=7
	2

i rozwiązać.... A dla podpunktu b) wyznaczy obliczyć wierzchołek dla |y₁−y₂|=d(x)

Ergo: A jak znaleźć ten wierzchołek |y₁−y₂|=d(x)

Ergo: