okrag
blogther: mam okrag o rownaniu ( x + 4 )2 + ( y − 1 )2 = 25 i prosta o rownaniu y = 34x + m mam
wyznaczyc zbior wszystkich liczb m dla ktorych prosta jest styczna do okregu
dlaczego zatem jak rozwiazuje cos takiego
( x + 4 )2 + ( 34x + m − 1 )2 = 25
i potem licze Δ = 0
bo jeden punkt wspolny nie wychodzi mi poprawna odpowiedz? gdzie robie bład?
7 kwi 22:18
krystek: sposób poprawny, może rachunkowy bład robisz.
7 kwi 22:20
Mila: To bardzo pracochłonny sposób.
Zrób z odległości punktu s(−4,1) od prostej w postaci ogólnej.
7 kwi 22:30
blogther: i co wtedy otrzymam MILA?
w odpowiedzi własnie robia tym sposobem ale ja nie wiem czego mam sie spodziewac sprobowałem
jeszcze raz to policzyc ale tym razem podstawiajac do rownania okregu ktore jeszcze nie
zostało uporzadkowane i tym sposobem wyszło w 16 linijkach na maturze nie bede miał tyle
czasu ani miejsca ale prawdopodobnie nie bedzie takiego zadania
7 kwi 22:33
7 kwi 22:36
blogther: tak znam ten wzor bede musił jeszcze napisac to rownanie prostej napisac w postaci ogolnej
7 kwi 22:37
blogther: rozumien ze d = r
i co mi to da ?
7 kwi 22:38
Eta:
S(−4,1) r=5 k: 0,75x−y+m=0
| | |−4*0,75+1*(−1)+m| | |
d= |
| = 5 |
| | √(0,75)2+(−1)2 | |
| | 25 | |
|m−4|= |
| ⇒ m=....... v m=..... |
| | 4 | |
7 kwi 22:38
blogther: czyli te punkty beda lezały po na krancach prostej o długości 2d czyli cienciwie tego okregu
tak
7 kwi 22:39
krystek: to masz m dla prostej aby była styczna do okręgu
7 kwi 22:44
blogther: ja sobie policze jeszcze raz tym sposobem i zadam wam pytanie jak czegos nie bede wiedział
7 kwi 22:47
blogther: czyli zamiast podstawiania do rownania okregu tej prostej to moge za kazdym razem wyznaczac
punkty przeciecia sie prostej z okregiem na przykład gdybym nie miał tego parametru m tylko
jakas liczbe to bede mogł zrobic tak jak teraz czy nie?
7 kwi 22:52
blogther: czy tylko ten sposob jest dla prostej ktora ma tylko jeden punkt wspolny z okregiem
7 kwi 22:53
blogther:
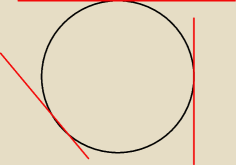
czyli w takim przypadku moge stosowac te metode
7 kwi 22:54
blogther:
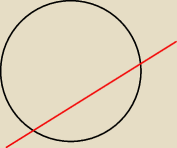
a w taki juz nie
7 kwi 22:55
Eta:
Można rozwiązać układ równań prostej i okręgu
i nałożyć warunek ,że Δ=0
(ten sposób jest bardziej pracochłonny w obliczeniach)
7 kwi 22:56
blogther: bo zazwyczaj jak szukałem punktow wspolnych prostej i okregu to podstawilem rownanie prostej
do rownania okregu wiec troche mnie dziwi ten sposob nie wiem czego sie po nim spodziewac mam
7 kwi 22:56
Eta:
d=r −−− to prosta styczna (1 punkt wspólny)
d >r −−− prosta nie ma punktów wspólnych z okręgiem
d<r −−−− prosta ma dwa punkty wspólne z okręgiem
7 kwi 22:58
blogther: a gdzybym miał taka prosta y = 3x − 2 i ten sam okrag i mam zrobic to samo ze ma pokazac punkty
stycznosci to robie ta samo metoda tak?
7 kwi 22:58
blogther: czyli za kazdym razem moge tak robic tylko poprzez zastosowanie odpowiedniego znaku rownosci
lub nierownosci bede wiedział co mam policzyc tak?
7 kwi 22:59
blogther: poszukam podobnych zadan i sprawdze czy ta metoda jest uniwersalna
7 kwi 23:00
krystek:
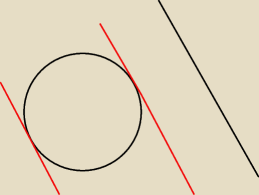
7 kwi 23:02
blogther: albo moze znacie jakies takie podobne zadania?
7 kwi 23:03
blogther: jak na złosc nie ma nic
7 kwi 23:04
krystek: w zbiorach i na info szukaj
7 kwi 23:04
krystek: wpisz na tym forum w wyszukiwarke− jest sporo zadań .
7 kwi 23:09
Eta:
zad1/ Sprawdź (rachunkowo) czy prosta y=2x+8
nie ma punktów wspólnych z okręgiem (x−3)2+(y+3)2=9
7 kwi 23:10
blogther: czyli jak mam taka prosta y = 2x + 8
i rownanie okregu (x − 2)2 + (y − 1)2 = 25
czyli jak policzyłym teraz z tego wzoru to znajde te punkty stycznosci
i to za kazdym razem zadziała tak?
( rownanie tej prostej i okregu wymysliłem teraz wiec akurat w tym przypadku moze nie byc
punktów wspolnych ale gdyby były to bedzie zachodziła rownosc tak? a jak nie bedzie rownosci
to nie ma punktow jak to jest?)
7 kwi 23:11
blogther: policzyłbym to ta metoda bardziej pracochłonna
7 kwi 23:11
7 kwi 23:14
blogther: wyszło mi cos takiego
| | − 50 − 4√5 | | − 50 + 4√5 | |
x1 = |
| lub x2 = |
|
|
| | 10 | | 10 | |
i teraz podstawiam do rownania okregu za x i sprawdzam czy zachodzi rownosc tak
7 kwi 23:17
blogther: czyli to Twojego zadania ETA powinienem dac tak d > r i to udowadniam
7 kwi 23:18
Eta:
Dokładnie tak

7 kwi 23:20
Mila: Narysuj okrąg i prostą y=3/4x w układzie współrzędnych.
Styczna będzie równoległa do niej, nie pytają Cię w których punktach.
zatem wystarczy rozważyć kiedy prosta y=3/4 x+m jest odległa od środka okręgu o promień.
Eta to wyliczyła.
Wzór na odległość punktu od prostej masz w tablicach.
przekształć równanie prostej do postaci bez ułamków, to mniej okazji do pomyłek.
y=3/4x+m
4y=3x+4m
3x−4y+4m=0
| | |3*(−4)−4*1+4m| | |
d=5= |
| |
| | √32+42 | |
dalej potrafisz.
podaj wynik
7 kwi 23:22
blogther: jak licze tym sposobem to wychodzi mi cos takiego
3√5 > 17 czyli sprzecznosc czyli sa punkty wspolne tak
7 kwi 23:22
blogther: m = 414 lub m = − 94
7 kwi 23:24
blogther: czyli nie mam jednak tych punktow wspolnych
7 kwi 23:26
blogther: bo d = 17√5 a r to jest to 3
7 kwi 23:27
Mila: Dobrze wyznaczyłeś m. O jakie punkty wspólne Ci chodzi?
| | 3 | | 41 | | 3 | | −9 | |
Są dwie styczne y= |
| x+ |
| i y= |
| x+ |
| |
| | 4 | | 4 | | 4 | | 4 | |
Kazda z nich ma jeden punkt wspólny z danym okręgiem.
7 kwi 23:31
Mila: To zadanie, które zadała Ci Eta lepiej rozwiązać Twoim I sposobem.( bo masz konkretną prostą, a
nie z parametrem)
7 kwi 23:33
blogther: o to zadanie od ETA
7 kwi 23:33
blogther: ale i tak dobrze udowodniłem
7 kwi 23:33
blogther: okey dzieki za pomoc wam wszystkim
7 kwi 23:34
 czyli w takim przypadku moge stosowac te metode
czyli w takim przypadku moge stosowac te metode
 a w taki juz nie
a w taki juz nie

