zadanie3 maciek: w trójkącie ABC mamy dane |bc|=a, |ac|=b. wyznacz długość boku AB wiedząc, że środkowe poprowadzone do boków BC i AC są do siebie prostopadłe.

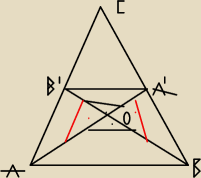
Basia: A' − środek BC B' − środek AC A'B' || AB i AB = 2A' B' tr. A'OB' i tr.AOB są podobne w skali 2 OA' = x ⇒ OA = 2x OB' = y ⇒ OB = 2y z tr.A'OB mamy x² + (2y)² = (^b₂)² z tr.B'OA mamy y² + (2x)² = (^a₂)²

	b2
x2 + 4y2 =
	4

	a2
4x2 + y2 =
	4

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	a2+b2
5x2 + 5y2 =		/:5
	4

	a2+b2
x2 + y2 =
	20

AB² = (2x)² + (2y)² AB² = 4x² + 4y² = 4(x²+y²)

	4(a2+b2)		a2 + b2
AB2 =		=
	20		5

AB = √^{a2 + b2}₅